Закон токов кирхгофа это

§ 15. Второй закон Кирхгофа. Применение законов Кирхгофа для расчета электрических цепей

При расчете электрических цепей часто приходится встречаться с цепями, которые образуют замкнутые контуры. В состав таких контуров, помимо сопротивлений, могут входить еще электродвижущие силы.

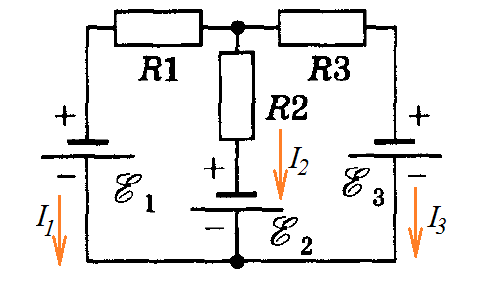
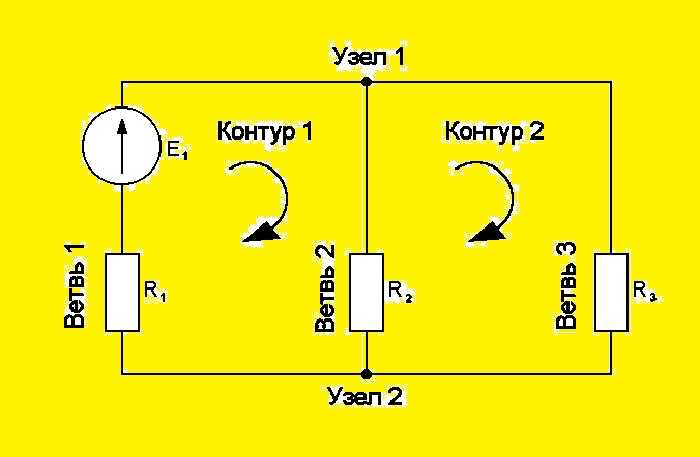
На рис. 35 представлена часть сложной электрической цепи в виде замкнутого контура АБВГ. На схеме указаны полярность электродвижущих сил E₁, E₂, E₃ и направления токов I₁, I₂, I₃ и I₄, протекающих на различных участках цепи.

Рис. 35. Участок сложной электрической цепи

Обходим контур от точки А в произвольном направлении, например по часовой стрелке. Рассмотрим каждый из участков рассматриваемого контура. На первом участке разность потенциалов между точками А и Б, или, что то же самое, напряжение U_AБ, равна э.д.с. Е₁ минус падение напряжения I₁r₁. Аналогично будет и на других участках цепи:

на участке АБ φА - φБ = Е1 - I1r1; 
на участке БВ φБ - φВ = -Е2 - I2r2; 
на участке ВГ φВ - φГ = E3 - I3r3; 
на участке ГА φГ - φА = I4r4.

Складывая левые и правые части уравнения, получим:

φ_A — φ_Б + φ_Б — φ_В + φ_В — φ_Г + φ_Г — φ_А = E₁ — I₁r₁ — E₂ — I₂r₂ + E₃ I₃r₃ + I₄r₄;
0 = E₁ — I₁r₁ — E₂ — I₂r₂ + E₃ — I₃r₃ + I₄r₄.

Перенося произведения (I⋅r) в одну часть, а электродвижущие силы (Е) в другую часть, получим

-E₁ + E₂ — E₃ = — I₁r₁ — I₂r₂ — I₃r₃ + I₄r₄.

Или в общем виде

ΣE = ∑I ⋅ r.

Это выражение представляет собой второй закон Кирхгофа. Формула показывает, что во всяком замкнутом контуре алгебраическая сумма электродвижущих сил равна алгебраической сумме падений напряжений.

По второму закону Кирхгофа,

∑E = ∑Ir.

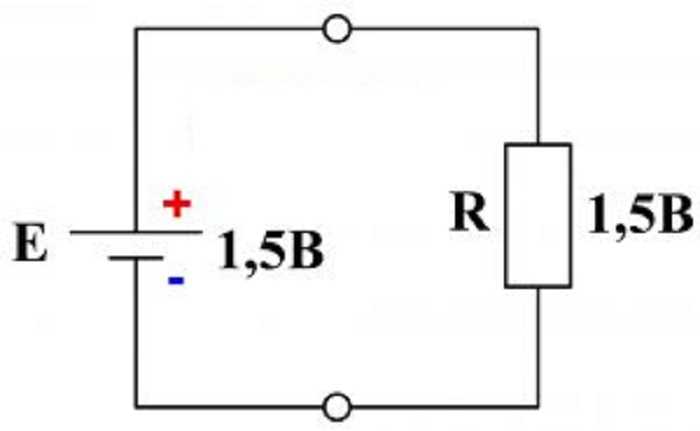
Для простейшей замкнутой цепи с одной э.д.с. Е (рис. 36)

E = Ir + Ir = I(r + r),

откуда

I = E/_r+r.

Рис. 36. Простой замкнутый контур

Мы получили формулу закона Ома для замкнутой цепи.

Следовательно, закон Ома является частным случаем 2-го закона Кирхгофа.

При расчете электрических цепей применяют различные методы расчета. Выбор того или иного метода зависит от конфигурации цепи, числа э.д.с., заданных величин.

Как правило, расчет неразветвленных цепей с любым числом э.д.с., а также расчет сложных цепей с одной э.д.с. легче производить, применяя закон Ома.

Расчет сложных цепей с несколькими э.д.с. производят с помощью уравнений 1-го и 2-го законов Кирхгофа.

Расчет сложной цепи методом законов Кирхгофа производят в следующем порядке:

Условно задаются направлениями токов в различных участках цепи.

Определяют число уравнений, которое необходимо составить для решения задачи. Если известны все э.д.с. и сопротивления цепи, число уравнений должно быть равно числу неизвестных токов.

Для составления уравнений вначале используют уравнения 1-го закона Кирхгофа. Число уравнений 1-го закона Кирхгофа на единицу меньше числа узловых точек в схеме. Остальное число уравнений составляют по 2-му закону Кирхгофа.

Для этого намечают контуры, направление обхода этих контуров и приступают к составлению уравнений. Если направление обхода не совпадает с направлениями э.д.с. или с направлениями токов на отдельных участках контура, то величины э.д.с. и падения напряжения I⋅r входят в уравнения со знаком минус.

Решая систему уравнений, находят величину токов,

Если окажется, что в результате решения уравнений некоторые из токов получились отрицательными, то это значит, что направление этих токов было выбрано неправильно. Надо изменить направление токов на схеме.

Проверка правильности решения производится путем подстановки полученных значений токов в одно из составленных уравнений.

Решим несколько задач, используя закон Ома и оба закона Кирхгофа.

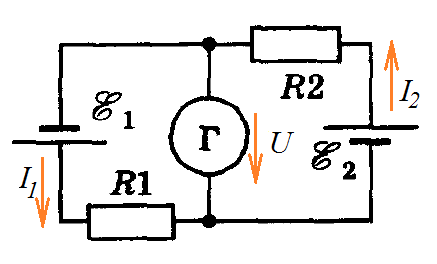
Пример 30. Найти токи в цепи, представленной на рис. 37. Выберем произвольно положительное направление тока. Обходя контур по часовой стрелке, пишем уравнение второго закона Кирхгофа:

-E₁ + E₂ = Ir₁ + Ir₂;
-1,9 + 1,3 = I(2 + 3);
-0,6 = 5I, I = -0,12 а.

Рис. 37. Электрическая цепь (к примеру 30)

Знак минус означает, что выбранное нами направление тока противоположно его действительному направлению.

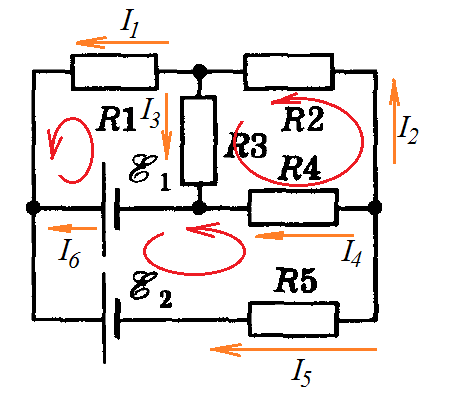
Пример 31. Дана электрическая цепь (рис. 38). Определить токи на отдельных участках.

Рис. 38. Электрическая цепь (к примеру 31)

Произвольно выбираем положительные направления токов.

Для контура абде

6 = 2I₁ + 5I₃. (1)

Для контура авге

6 — 2 = 2I₁ — 4I₂. (2)

Для точки б, по первому закону Кирхгофа,

I₃ = I₁ + I₂. (3)

Имеем три уравнения с тремя неизвестными. Решая их, находим величину и направление токов. Подставляя значение тока I₃ из уравнения (3) в уравнение (1), получим

 6 = 2I1 + 5I1 + 5I2;
 6 = 7I1 + 5I2 
+
 2 = I1 - 2I2

или

 12 = 14I1 + 10I2 
+ 
 10 = 5I1 + 10I2.

Складывая два последних уравнения, имеем:

22 = 19I₁, откуда I₁ = 1,156 а,

подставляем значение I₁ в уравнение (1):

6 = 2 ⋅ 1,156 + 5I₃,

I3 =	6 — 2 ⋅ 1,156	= 0,74 а.
5

Подставляем значение I₁ в уравнение (2):

2 = 1,156 — 2I₂,

откуда

I2 =	— 2 + 1,156	= — 0,422 a.
2

Знак минус показывает, что действительное направление тока I₂ обратно принятому нами направлению.

Термины

• Электродвижущая сила (ЭДС) – напряжение, сформированное батареей или магнитной силой в соответствии с законом Фарадея.
• Резистор – электрический компонент, передающий ток в прямой пропорциональности напряжению.

Правило напряжения второго закона Кирхгофа относится к электрическим схемам и основывается на принципе сбережения энергии (энергия не создается и не уничтожается). Если рассматриваем схему, то речь идет о том, что направленная сумма разностей электрических напряжений вокруг замкнутой сети приравнивается к нулю. То есть, сумма значений электродвижущей силы в замкнутой петле достигает суммы потенциальных потерь в ней.

Можно также сказать, что алгебраическая сумма созданных сопротивлений в замкнутой системе приравнивается к общей ЭДС. В математическом виде уравнение по второму закону Кирхгофа:

(V_k – напряжение на элементе k, а n – общее количество элементов в замкнутой цепи). В нижнем примере сумма v₁, v₂, v₃ и v₄ (и v₅, если включена) приравнивается к 0.

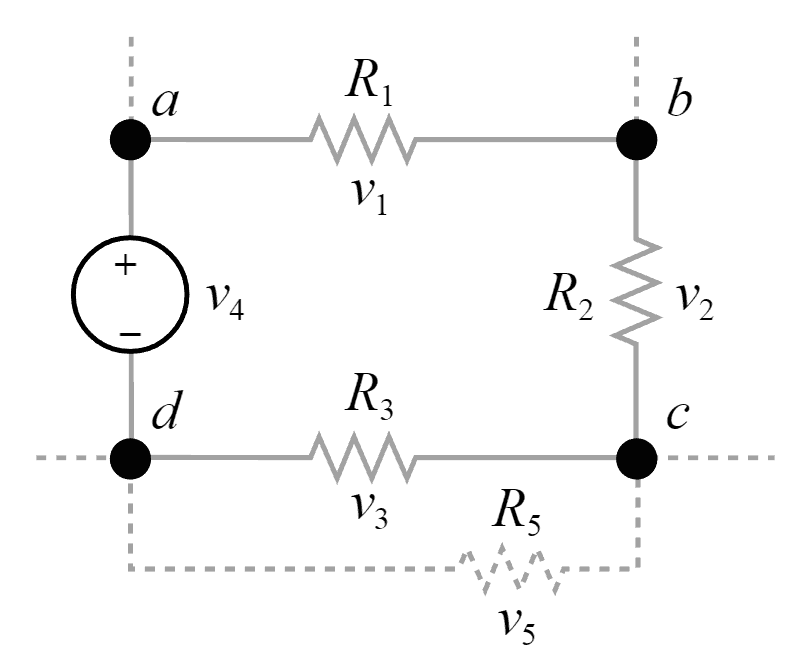
Сумма всех напряжений в цикле приравнивается к нулю: v₁, v₂, v₃ и v₄ = 0

Второе правило Кирхгофа основывается на законе сохранения энергии: общая энергия, полученная на единицу заряда, должна приравниваться к количеству потерянной энергии.

Постоянный ток: законы Кирхгофа

При решении задач на законы Кирхгофа лучше придерживаться определенного алгоритма: 1. определить число неизвестных токов – столько уравнений должно быть в системе ; 2. определить количество узлов – уравнений по первому закону тогда нужно составить на одно меньше; 3. проложить контуры и записать для них уравнения по второму закону. Кто хочет разобраться досконально – есть видео.

Задача 1. Два элемента с В и В соединены по схеме, показанной на рисунке . Сопротивление Ом. Внутреннее сопротивление элементов одинаково Ом. Определить силу тока, идущего через сопротивление .

К задаче 1

Обозначим токи в ветвях произвольно. По первому закону Кирхгофа сумма токов, сходящихся в узле, равна 0:

Будем обходить верхний контур против часовой стрелки. По второму закону Кирхгофа сумма падений напряжений в контуре равна сумме ЭДС:

Будем обходить второй контур по часовой стрелке:

Неизвестных токов – три, мы составили три уравнения. Этого достаточно, чтобы найти токи:

Выразим из второго уравнения, а – из третьего:

Подставим эти выражения в первое уравнение:

Тогда токи и

Ответ: A, A, A. Задача 2. Найти силу тока на всех участках цепи‚ если В, В‚ В, Ом‚ Ом‚ Ом‚ Ом‚ Ом, Ом.

К задаче 2

Обозначаем токи в ветвях произвольно, выбираем направления обходов контуров и сами контуры. Составляем систему уравнений. Сначала составим уравнение по первому закону Кирхгофа – у нас два узла, поэтому уравнение будет одно. Затем, обходя контуры, составим два уравнения по второму закону: их нужно составить два, так как неизвестных токов в цепи три.

Решаем систему и находим ответ (я решала с помощью он-лайн калькулятора): , , .

Ответ: , , .

Задача 3. В схеме, показанной на рисунке, найти силу тока через гальванометр, если В, кОм; В, кОм. Сопротивлением гальванометра пренебречь.

К задаче 3

Нам неизвестно сопротивление гальванометра, запишем для напряжения на нем два уравнения:

Приравнивая, получим

Заметим, что, если , то равенство будет выполнено. Таким образом, ток через гальванометр не течет.

Ответ: .

Задача 4. В цепи В‚ В, Ом, Ом. Найти распределение токов в цепи. Внутреннее сопротивление источников тока не учитывать.

К задаче 4

Обозначаем токи в ветвях произвольно, выбираем направления обходов контуров и сами контуры. Составляем систему уравнений. Сначала составим уравнение по первому закону Кирхгофа – у нас три узла, поэтому уравнений будет два. Затем, обходя контуры, составим три уравнения по второму закону: их нужно составить именно три, так как неизвестных токов в цепи шесть.

Решаем систему и находим ответ (я решала с помощью он-лайн калькулятора): , , , , , .

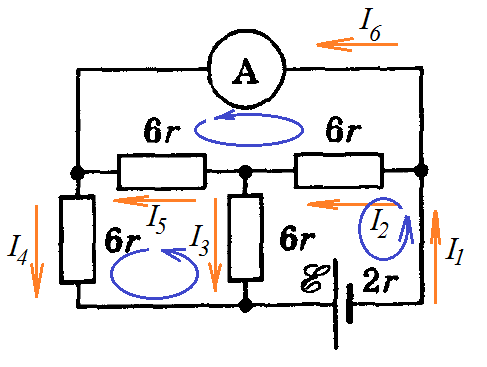
Ответ: , , , , , . Задача 5. Какую силу тока покажет амперметр в схеме, изображенной на рисунке? Сопротивлением амперметра пренебречь.

К задаче 5

Обозначим токи в цепи произвольно. Обозначим направления обхода контуров. Запишем систему уравнений: составим три уравнения по первому закону (на одно меньше, чем количество узлов) и три уравнения по второму закону, так как неизвестных токов шесть и система должна состоять из шести уравнений.

Чтобы воспользоваться калькулятором, я задала Ом и В. В итоге получилось: , , , , , .

Минусы свидетельствуют о противоположном направлении тока в этой ветви тому, что мы нарисовали.

Законы Кирхгофа и их физический смысл. Расчет ЭЦ методом законов Кирхгофа. Баланс мощностей.

Элементы и структура ЭЦ. Режимы работы реального генератора ЭДС. Условие передачи максимальной мощности от генератора к нагрузке. Режим согласования. Замена реального генератора тока генератором ЭДС.

Электрическая цепь состоит из отдельных частей, выполняющих определенные функции и называемых элементами цепи. Основными элементами цепи являются источники и приемники электрической энергии. Электротехнические устройства, производящие электрическую энергию, называются генераторами или источниками электрической энергии, а устройства, потребляющие ее – приемниками электрической энергии.

Различают двух –и многополюсные элементы. Двухполюсники имеют два зажима. К ним относятся источники энергии, резисторы, катушки индуктивности, конденсаторы. Многополюсные элементы – это, например, триоды, трансформаторы, усилители и т.д.

В общем случае внешней характеристикой источника (т.е. зависимость напряжения от тока) является нелинейной (кривая 1 на рис. 4,б). Она имеет две характерные точки, которые соответствуют:

а – режиму холостого хода .

б –режиму короткого замыкания

Прямая 2 на рис. 4,б описывается линейным уравнением

Кроме отмеченных режимов функционирования источника, на практике важное значение имеет согласованный режим работы, при котором нагрузкой RН от источника потребляется максимальная мощность

Условие такого режима

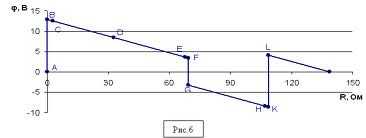
Разность потенциалов между двумя точками электрической цепи. Потенциальная диаграмма.

Разность потенциалов считается по формуле точке (б), идя от точки (а): fi(b)=fi(a)+R*I.

Под потенциальной диаграммой понимают график распределения потенциала вдоль какого-либо участка цепи или замкнутого контура. По оси абсцисс на нем откладывают сопротивления вдоль контура, начиная с какой-либо произвольной точки, по оси ординат — потенциалы. Каждой точке участка цепи или замкнутого контура соответствует своя точка на потенциальной диаграмме.

Преобразование пассивных ЭЦ (последовательное и параллельное соединение, треугольник-звезда и звезда-треугольник).

Законы Кирхгофа и их физический смысл. Расчет ЭЦ методом законов Кирхгофа. Баланс мощностей.

Первый закон Кирхгофа – алгебраическая сумма всех токов, сходящихся в любом узле, равна нулю

Положительные направления токов каждой ветви произвольны. Токи направленные к узлу принимаются отрицательными, направленные от него – положительными (или наоборот).

Второй закон Кирхгофа – алгебраическая сумма ЭДС в любом замкнутом контуре равна алгебраической сумме падений напряжений в нем.

Направление обхода контура произвольно. При записи левой части равенства те ЭДС, направления которых совпадают с направлением обхода контура принимаются положительными; ЭДС, направленные против выбранного направления обхода – отрицательными. При записи правой части равенства со знаком плюс берутся падения напряжения на тех элементах r_kчерез которые протекают токи i_k, положительное направление которых совпадает c направлением обхода и со знаком минус – падения напряжения на тех элементах, через которые протекают токи, положительное направление которых противоположно направлению обхода.

Порядок анализа на основании законов Кирхгофа

1. Определить число неизвестных токов, равное N_B — N_J. 2.Указать положительное направление тока в каждой ветви. 3. Составить N₁ = N _у — 1 независимых уравнений по первому закону Кирхгофа. 4. Составить N₂ = N_В — N_J — (N_У — 1) независимых уравнений по второму закону Кирхгофа. При составлении уравнений по второму закону Кирхгофа следует выбирать лишь те контуры, которые не содержат ветвей с источниками тока. Указать направление обхода контуров. 5. Число уравнений равно числу неизвестных токов N₁ + N₂ = N_В — N_J.

Баланс мощностей можно сформулировать так: алгебраическая сумма мощностей источников, должна быть равна арифметической сумме мощностей нагрузок. Если направление ЭДС и направление тока ветви не совпадают, то составляющая мощности этого источника в балансе мощностей берется со знаком «минус».

Источник



История

Пополнил ряды немецких ученых Кирхгоф в девятнадцатом столетии, когда в стране, находившаяся на пороге революции индустриальной, требовались новейших технологии. Ученые занимались поиском решений, которые могли бы ускорить развитие промышленности.

Активно занимались исследованиями в области электричества, поскольку понимали, что в будущем оно будет широко использоваться. Проблема состояла на тот момент не в том, как составлять электрические цепи из возможных элементов, а в проведении математических вычислений. Тут и появились законы, сформулированные физиком. Они очень помогли.

К узлу подходят 2 провода, а отходит один. Значение тока, текущего от узла, такое же, как сумма его, протекающего по двум остальным проводникам, т.е. идущим к нему. Правило Кирхгофа объясняет, что, при ином раскладе, накапливался бы заряд, но такого не бывает. Все знают, что всякую сложную цепь легко разделить на отдельные участки.

Но, при этом непросто определить путь, по которому он проходит. Тем более, что на различных участках сопротивления не одинаковы, поэтому и распределение энергии не будет равномерным.

В соответствие со Вторым правилом Кирхгофа, энергия электронов на каждом из замкнутых участков электрической цепи равняется нулю – нулю равняется всегда в таком контуре суммарное значение напряжений. Если бы нарушилось данное правило, энергия электронов при прохождении определенных участков, уменьшалась бы или увеличивалась. Но, этого не наблюдается.

Второй закон Кирхгофа.

Формулировка: Алгебраическая сумма ЭДС, действующих в замкнутом контуре, равна алгебраической сумме падений напряжения на всех резистивных элементах в этом контуре.

Здесь термин «алгебраическая сумма» означает, что как величина ЭДС так и величина падения напряжения на элементах может быть как со знаком «+» так и со знаком «-». При этом определить знак можно по следующему алгоритму:

1. Выбираем направление обхода контура (два варианта либо по часовой, либо против).

2. Произвольно выбираем направление токов через элементы цепи.

3. Расставляем знаки для ЭДС и напряжений, падающих на элементах по правилам:

— ЭДС, создающие ток в контуре, направление которого совпадает с направление обхода контура записываются со знаком «+», в противном случае ЭДС записываются со знаком «-».

— напряжения, падающие на элементах цепи записываются со знаком «+», если ток, протекающий через эти элементы совпадает по направлению с обходом контура, в противном случае напряжения записываются со знаком «-».

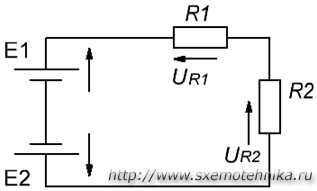
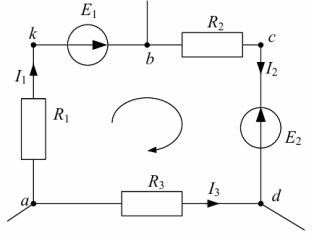
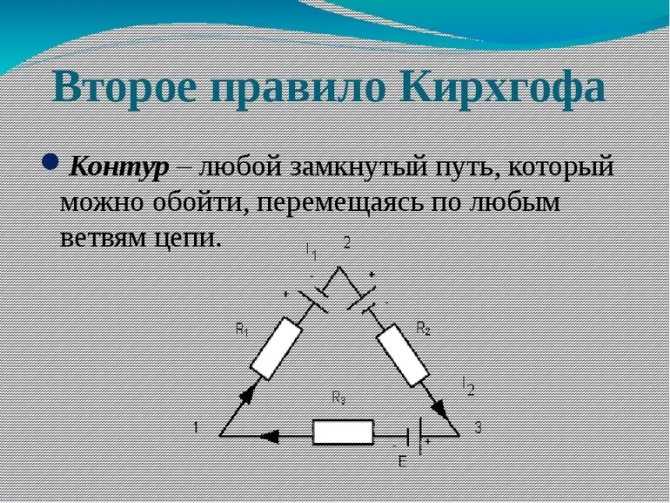
Например, рассмотрим цепь, представленную на рисунке 3, и запишем выражение согласно второму закону Кирхгофа, обходя контур по часовой стрелке, и выбрав направление токов через резисторы, как показано на рисунке.

Рисунок 3. Электрическая цепь, для пояснения второго закона Кирхгофа.

Предлагаю посмотреть отдельный видеоурок по второму закону Кирхогфа (теория).

Формулировка правил

Каждое правило Кирхгофа обладает универсальными свойствами. Как первое, так и второе, хоть и не относятся к фундаментальным законам, но твёрдо обоснованы.

Определения

Прежде, чем рассматривать простые принципы и смысл решения СУ (систем уравнений), нужно определиться с применяемыми формулировками. В типологии цепей пользуются следующими понятиями:

• ветвь;
• узел;
• контур.

Всё это – элементы электрической цепи (ЭЦ).

Часть электроцепи, через которую проходит электричество одной и той же величины, называется ветвью. Место, в котором соединяются три и более ветви, именуют узлом. Обычно на схемах узлы обозначаются крупными точками. Контуром называется путь, по которому протекает электрический ток, проходя через несколько участков ЭЦ, включающих в себя узлы и ветви.

Важно! Ток (I), выходя из одной точки контура и единожды проходя по разветвлениям и узлам, должен обязательно вернуться в начало. Контур – это замкнутая цепь

Узлы и ветви, подлежащие изучаемому в определённый момент контуру, могут входить в состав других контуров: являться общими для нескольких замкнутых ЭЦ одновременно.

Первое правило

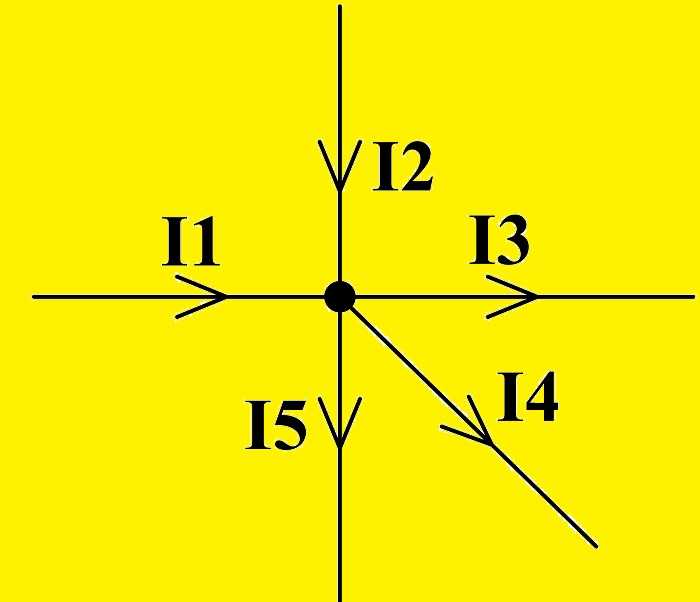
Первая закономерность Кирхгофа звучит так: «Сумма всех токов в узлах ЭЦ равна нулю». Если придать направление токам, текущим сквозь пересечения проводников, имеющих общий контакт (узел), то можно промаркировать стрелками, указывающими на узел, втекающие токи. Стрелками, имеющими направленность от узла, удобно отмечать вытекающие токи:

I1 + I2 – I3 – I4 – I5 = 0

Условно считая, что входящие I имеют плюсовой знак, а выходящие – минусовой, можно перефразировать утверждение. Согласно закону сохранения заряда, алгебраические суммы входящих в узел и выходящих из него I по значению равны.

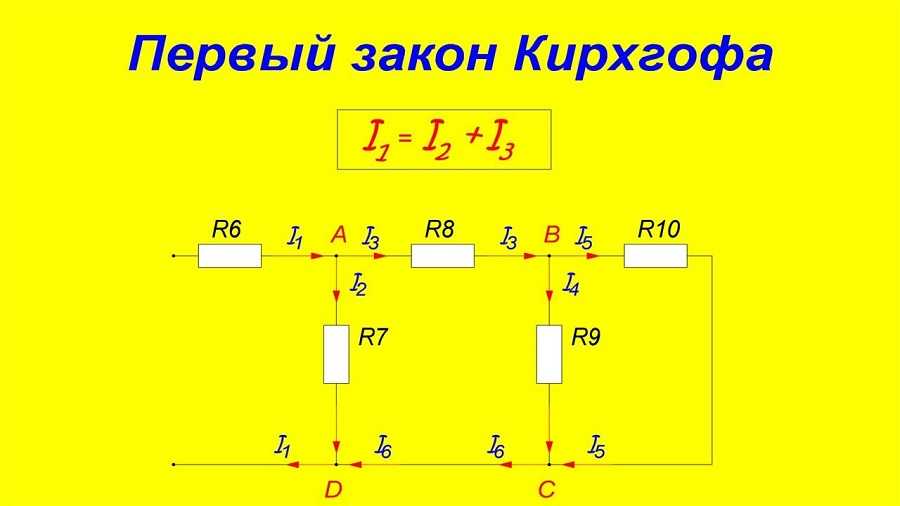
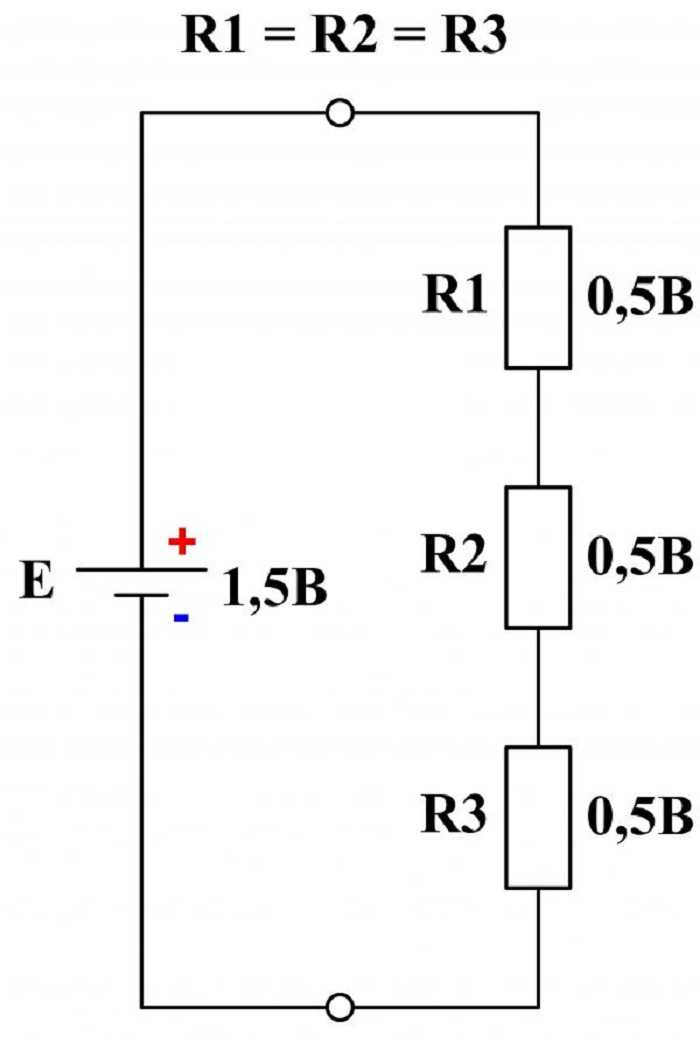
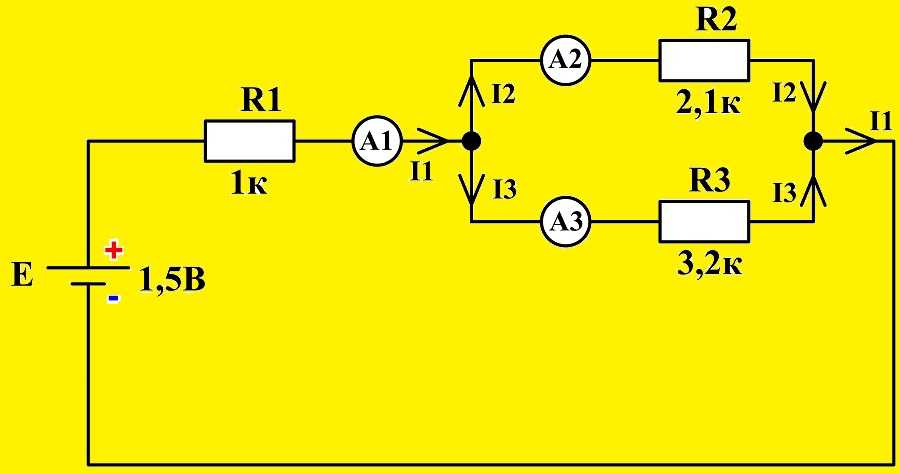
Убедиться в истинности первого правила можно, собрав смешанную схему включения резисторов, в качестве нагрузки, для источника питания U = 3 В.

Включенные в ветви амперметры позволяют визуально зафиксировать значения токов, входящих и выходящих из первого узла. Их алгебраическая сумма (учитывая знаки) будет равна нулю.

Второе правило

Его называют правилом напряжений, оно утверждает, что сумма всех E (ЭДС), входящих в контур, равняется сумме падений напряжений на резистивных элементах, при условии, что контур замкнутый:

Например, для цепи с элементом питания и резистором напряжение на резисторе U = I*R будет равно ЭДС батарейки. По второму определению Кирхгофа выражение будет иметь вид:

По аналогии, если количество резисторов увеличить, то падение напряжения на них распределится так, что в сумме они сравняются со значением ЭДС источника питания:

E = I*R1 + I*R2 + I*R.

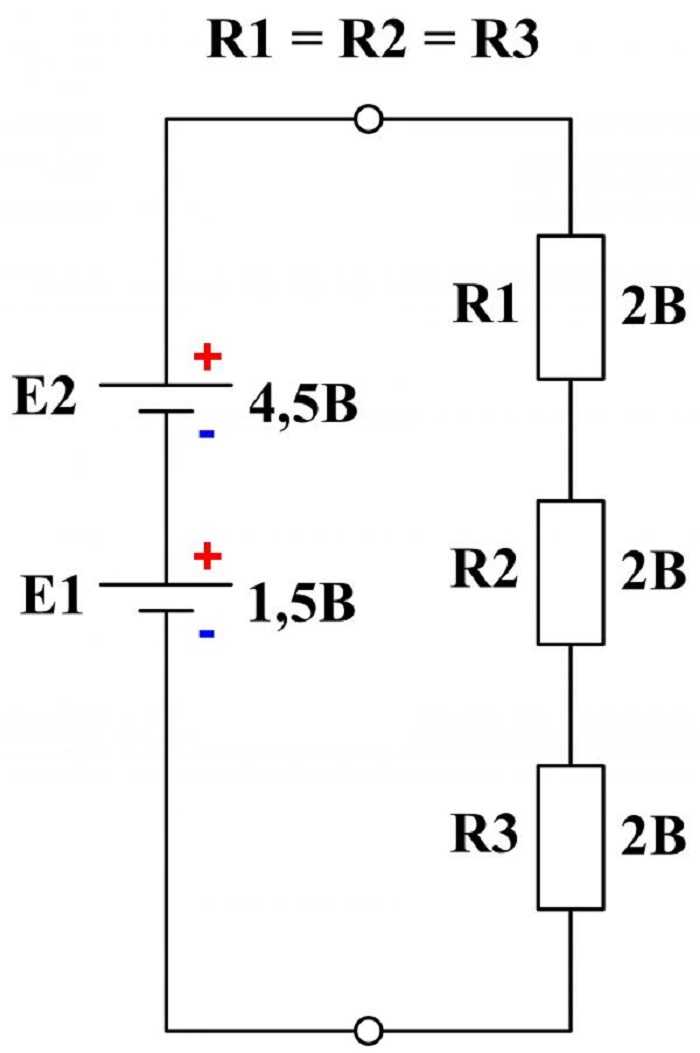
Объяснение было бы не полным, если не рассмотреть схему с несколькими ЭДС, входящими в контур. В этом случае выражать равенство следует следующим образом:

E1 + E2 = I*R1 + I*R2 + I*R3.

К сведению. При подключении нескольких источников в один контур необходимо соблюдать полярность, выполняя последовательное соединение плюса одного источника с минусом другого, таким образом, значения ЭДС будут суммироваться.

Законы Кирхгофа — формулы и примеры использования

Законы Кирхгофа устанавливают соотношения между токами и напряжениями в разветвленных электрических цепях произвольного типа. Законы Кирхгофа имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения любых электротехнических задач. Законы Кирхгофа справедливы для линейных и нелинейных цепей при постоянных и переменных напряжениях и токах.

Первый закон Кирхгофа вытекает из закона сохранения заряда. Он состоит в том, что алгебраическая сумма токов, сходящихся в любом узле, равна нулю.

где – число токов, сходящихся в данном узле. Например, для узла электрической цепи (рис. 1) уравнение по первому закону Кирхгофа можно записать в виде I1 — I2 + I3 — I4 + I5 = 0

В этом уравнении токи, направленные к узлу, приняты положительными.

Физически первый закон Кирхгофа – это закон непрерывности электрического тока.

Второй закон Кирхгофа: алгебраическая сумма падений напряжений на отдельных участках замкнутого контура, произвольно выделенного в сложной разветвленной цепи, равна алгебраической сумме ЭДС в этом контуре

где k – число источников ЭДС; m – число ветвей в замкнутом контуре; Ii , Ri – ток и сопротивление i -й ветви.

Так, для замкнутого контура схемы (рис. 2 ) Е1 — Е2 + Е3 = I1R1 — I2R2 + I3R3 — I4R4

Замечание о знаках полученного уравнения:

1) ЭДС положительна, если ее направление совпадает с направлением произвольно выбранного обхода контура;

2) падение напряжения на резисторе положительно, если направление тока в нем совпадает с направлением обхода.

Физически второй закон Кирхгофа характеризует равновесие напряжений в любом контуре цепи.

Расчет разветвленной электрической цепи с помощью законов Кирхгофа

Метод законов Кирхгофа заключается в решении системы уравнений, составленных по первому и второму законам Кирхгофа.

Метод заключается в составлении уравнений по первому и второму законам Кирхгофа для узлов и контуров электрической цепи и решении этих уравнений с целью определения неизвестных токов в ветвях и по ним – напряжений. Поэтому число неизвестных равно числу ветвей b , следовательно, столько же независимых уравнений необходимо составить по первому и второму законам Кирхгофа.

Число уравнений, которые можно составить на основании первого закона, равно числу узлов цепи, причем только ( y – 1) уравнений являются независимыми друг от друга.

Независимость уравнений обеспечивается выбором узлов. Узлы обычно выбирают так, чтобы каждый последующий узел отличался от смежных узлов хотя бы одной ветвью. Остальные уравнения составляются по второму закону Кирхгофа для независимых контуров, т.е. число уравнений b — (y — 1) = b — y +1 .

Контур называется независимым, если он содержит хотя бы одну ветвь, не входящую в другие контуры.

Составим систему уравнений Кирхгофа для электрической цепи (рис. 3 ). Схема содержит четыре узла и шесть ветвей.

Поэтому по первому закону Кирхгофа составим y — 1 = 4 — 1 = 3 уравнения, а по второму b — y + 1 = 6 — 4 + 1 = 3 , также три уравнения.

Произвольно выберем положительные направления токов во всех ветвях (рис. 4 ). Направление обхода контуров выбираем по часовой стрелке.

Составляем необходимое число уравнений по первому и второму законам Кирхгофа

Полученная система уравнений решается относительно токов. Если при расчете ток в ветви получился с минусом, то его направление противоположно принятому направлению. Потенциальная диаграмма – это графическое изображение второго закона Кирхгофа, которая применяется для проверки правильности расчетов в линейных резистивных цепях. Потенциальная диаграмма строится для контура без источников тока, причем потенциалы точек начала и конца диаграммы должны получиться одинаковыми.

Рассмотрим контур abcda схемы, изображенной на рис. 4. В ветке ab между резистором R1 и ЭДС E1 обозначим дополнительную точку k.

Рис. 4. Контур для построения потенциальной диаграммы

Потенциал любого узла принимаем равным нулю (например, ?а= 0), выбираем обход контура и определяем потенциалы точек контура: ?а = 0, ?к = ?а — I1R1 , ? b = ? к + Е1, ?с = ? b — I2R2 , ? d = ?c — Е2, ? a = ?d + I3R3 = 0

При построении потенциальной диаграммы необходимо учитывать, что сопротивление ЭДС равно нулю (рис. 5 ).

Рис. 5. Потенциальная диаграмма

Законы Кирхгофа в комплексной форме

Для цепей синусоидального тока законы Кирхгофа формулируются так же, как и для цепей постоянного тока, но только для комплексных значений токов и напряжений.

Первый закон Кирхгофа : «алгебраическая сумма комплексов тока в узле электрической цепи равна нулю»

Второй закон Кирхгофа : «в любом замкнутом контуре электрической цепи алгебраическая сумма комплексных ЭДС равна алгебраической сумме комплексных напряжений на всех пассивных элементах этого контура».

Источник

Учебные материалы

Согласно первому закону Кирхгофа алгебраическая сумма токов ветвей, сходящихся в узле, равна нулю:

Согласно второму закону Кирхгофа алгебраическая сумма напряжений на резистивных элементах замкнутого контура равна алгебраической сумме ЭДС, входящих в этот контур.

Расчет многоконтурной линейной электрической цепи, имеющей «b» ветвей с активными и пассивными элементами и «у» узлов, сводится к определению токов отдельных ветвей и напряжений на зажимах элементов, входящих в данную цепь.

Пассивной называется ветвь, не содержащая источника ЭДС. Ветвь, содержащая источник ЭДС, называется активной.

1-й закон Кирхгофа применяют к независимым узлам, т.е. таким, которые отличаются друг от друга хотя бы одной новой ветвью, что позволяет получить (y — I) уравнений.

Недостающие уравнения в количестве b — (у — I) составляют, исходя из второго закона Кирхгофа. Уравнение записывают для независимых контуров, которые отличаются один от другого, по крайней мере, одной ветвью.

Порядок выполнения расчета:

1. выделяют в электрической цепи ветви, независимые узлы и контуры;
2. с помощью стрелок указывают произвольно выбранные положительные направления токов в отдельных ветвях, а также указывают произвольно выбранное направление обхода контура;
3. составляют уравнения по законам Кирхгофа, применяя следующее правило знаков:
   1. токи, направленные к узлу цепи, записывают со знаком «плюс», а токи, направленные от узла,- со знаком «минус» (для первого закона Кирхгофа);
   2. ЭДС и напряжение на резистивном элементе (RI) берутся со знаком»плюс», если направления ЭДС и тока в ветви совпадают с направлением обхода контура, а при встречном направлении — со знаком «минус»;
4. решая систему уравнений, находят токи в ветвях. При решении могут быть использованы ЭВМ, методы подстановки или определителей.

Отрицательные значения тока какой-либо ветви указывают на то, что выбранные ранее произвольные направления тока оказались ошибочными. Это следует учитывать, например, при построении потенциальной диаграммы, где следует знать истинное направление тока.

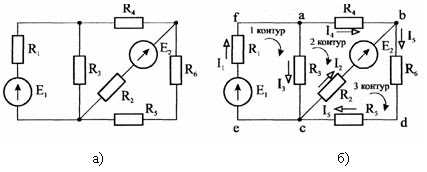
На рис. 4, а изображена исходная электрическая схема, для которой следует рассчитать токи в ветвях. Направления токов и обхода контуров приведены на рис. 4, б.

Система уравнений, составленных по первому и второму законам Кирхгофа, имеет вид

Источник

Первое и второе правила Кирхгофа

Первоначальной функцией законов Кирхгофа является расчет электрических цепей.

Для описания законов вводятся следующие понятия:

1. Узел — точка, являющаяся местом соединения нескольких проводников гальванической цепи.
2. Ветвь — участок схемы цепи, расположенный между 2 узлами. По ней протекает электрический ток с разными зарядами, но одинаковой силой.
3. Контур — закрытый путь, пересекающий несколько ветвей и узлов разветвленной гальванической цепи.

Ветвь и узел способны быть как частями единого контура, так и отдельными элементами нескольких замкнутых путей.

Формулировка первого правила Кирхгофа для разветвленных цепей: в электрических схемах с последовательным соединением источника и приемника энергии суммарное количество токов, текущих по направлению к узлу, эквивалентно общему числу токов, текущих по направлению от узлов. Поток энергии, направленный к узлу, является положительным. Поток частиц, направленных от узла, является отрицательным.

При сложении 2 противоположно направленных токов с одинаковой величиной будет всегда получаться 0. Физический смысл первого закона заключается в том, что заряд не концентрируется в узлах гальванической схемы.

Для расчета силы постоянного тока используется следующая формула: I 1 =I 2 +I 3. При использовании первого правила для расчета переменного тока дополнительно применяются величины мгновенного напряжения. Формула записывается в комплексной форме с учетом активных и реактивных составляющих.

Второй закон Кирхгофа является следствием 3 уравнения Максвелла, доказывающего отсутствие магнитных зарядов в природе. Определение второго правила Кирхгофа: на резисторах закрытого контура гальванической цепи сумма напряжений эквивалентна общему числу ЭДС (электродвижущей силы), рассчитанной для замкнутого пути. Если в составе электрической схемы не присутствуют приборы, вырабатывающие ЭДС, то сумма напряжений будет равняться 0.

Электродвижущая сила равномерно распределяется на всех узлах электрической цепи. Отдельным случаем второго правила является закон Ома, описывающий соотношение ЭДС и силы тока в проводнике.

Второй закон применяется к переменному току.

В этом случае суммарное количество амплитуд ЭДС эквивалентно общей сумме падений напряжений на всех частях гальванической цепи.

При составлении линейных уравнений для второго закона необходимо правильно определить направление падения напряжений.

Для указания знака этой величины был разработан алгоритм:

1. Отбирается направление обхода замкнутого пути. Падение способно двигаться по или против часовой стрелки.
2. Выбирается направление движения потоков энергии, текущих через основные части электрической цепи.
3. Если направление обхода контура совпадает с направлением ЭДС, то ставится положительный знак. Если направления не совпадают, то ставится отрицательный символ.