Параллельное соединение резисторов, а также последовательное

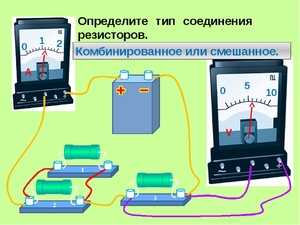
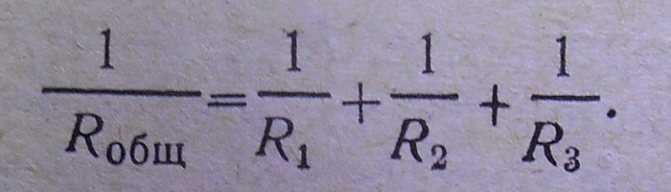Смешанное соединение резисторов

Пример решения задач

Дано:

U = 60 В

R₁ = 7 Ом

R₂ = 12 Ом

R₃ = 4 Ом

Найти: I₁; I₂; I₃ = ?

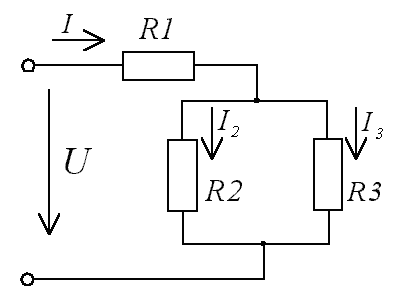
Резисторы R2 и R3 параллельны между собой, и их общее сопротивление R_2-3 последовательно с R₁.

R_вх = R₁ + R_{2 — 3}

R

_вх =R₁+R_2∙3= 7 + 3 = 10 Ом

I₁ = I

_вх = 6 А

U_{2 — 3} = I∙R_{2 — 3} — находим напряжение разветвленного участка:

U_{2 — 3} = I∙R_{2 — 3} = 6∙3 = 18 В

U_{2 — 3} = U₂ = U₃ =18 В

А

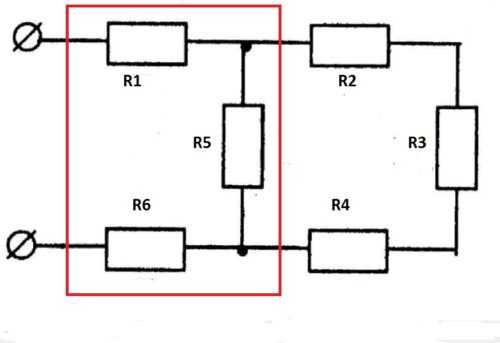
Дано:

U=240 В

R₁ = 20 Ом

R₂ = 120 Ом

R₃ = 40 Ом

R₄ = 60 Ом

R₅ = 30 Ом

R₆ = 20 Ом

Найти: I

_1-6 -?

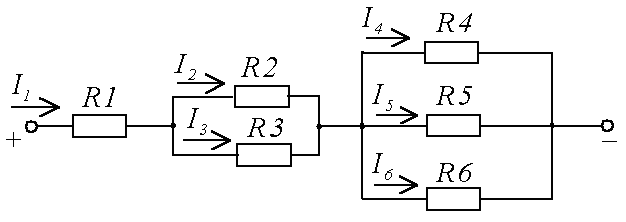
; R_4-6 = 10 Ом;

;

; R_2-3 = 30 Ом

R_вх=R₁+R_2-3+R_4-6 = 20 + 30 +10 = 60 Ом;

; ;

U_2-3 =I∙R_2-3= 4∙30 = 120 В;

U_{2 — 3} = U₂ = U₃;

;

;

U_4-6=I∙R_4-6=4∙10=40B;

U_4-6=U₄=U₅=U₆;

;

;

;

Дано:

E =

В

R_i=2Ом

R₁ =

Ом

R₂ =

Ом

R₃ =

Ом

R₄ =

Ом

R₅ =

Ом

R₆ = 1 Ом

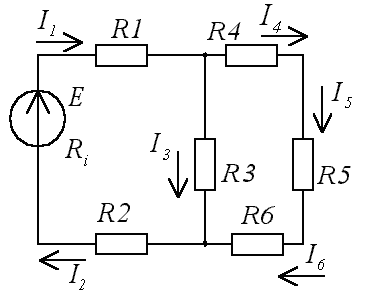
R_4-6 = R₄ + R₅ + R₆;

;

R_3-6 = 3 Ом;

R_вх = R₁ + R_3-6 +R₂ = 9 + 3 + 6 = 18 Ом;

I=;

I=I₁=I₂=1А;

U_3-6=I∙R_3-6=1∙3=3В;

U_3-6=U₃=U_4-6;

I₃=;

I₄=I₅=I₆=;

Cоставим подробное уравнение баланса мощностей для данной схемы. Оно является проверкой правильности решения задачи.

P_u=P_н+Р;

EI=I2₁∙R₁+ I2₂∙R₂+ I2₃R₃+I₄2R₄+I2₅R₅+I2₆+I2Ri;

20∙1=12∙9+12∙6+(0,25)2∙12+(0,75)2∙1+(0,75)22+(0,75)21+12∙2;

20Вт=20Вт- задача решена верно

ТОЭЭ  
к библиотеке  
к оглавлению  

Знаете ли Вы, что любой разумный человек скажет, что не может быть улыбки без кота и дыма без огня, что-то там, в космосе, должно быть, теплое, излучающее ЭМ-волны, соответствующее температуре 2.7ºК. Действительно, наблюдаемое космическое микроволновое излучение (CMB) есть тепловое излучение частиц эфира, имеющих температуру 2.7ºK. Еще в начале ХХ века великие химики и физики Д. И. Менделеев и Вальтер Нернст предсказали, что такое излучение (температура) должно обнаруживаться в космосе. В 1933 году проф. Эрих Регенер из Штуттгарта с помощью стратосферных зондов измерил эту температуру. Его измерения дали 2.8ºK — практически точное современное значение. Подробнее читайте в FAQ по эфирной физике.

НОВОСТИ ФОРУМАРыцари теории эфира

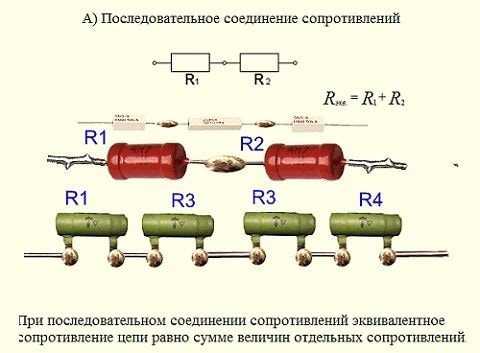
Последовательное соединение проводников

Сопротивление при последовательном соединении проводников

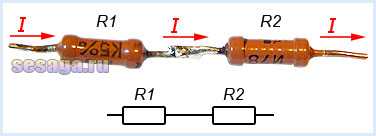
Последовательное соединение проводников – это когда к одному проводнику мы соединяем другой проводник и так по цепочке. Это и есть последовательное соединение проводников. Их можно соединять с друг другом сколь угодно много.

последовательное соединение резисторов

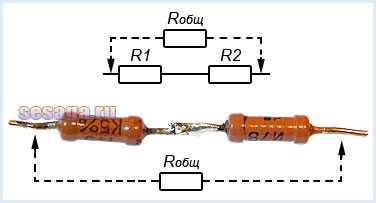
Чему же будет равняться их общее сопротивление? Оказывается, все просто. Оно будет равняться сумме всех сопротивлений проводников в этой цепи.

Получается, можно записать, что

формула при последовательном соединении резисторов

Пример

У нас есть 3 проводника, которые соединены последовательно. Сопротивление первого 3 Ома, второго 5 Ом, третьего 2 Ома. Найти их общее сопротивление в цепи.

Решение

R_общее =R₁ + R₂ + R₃ = 3+5+2=10 Ом.

То есть, как вы видите, цепочку из 3 резисторов мы просто заменили на один резистор R_AB .

показать на реальном примере с помощью мультиметра
Видео где подробно расписывается про эти соединения:

Сила тока через последовательное соединение проводников

Что будет, если мы подадим напряжение на концы такого резистора? Через него сражу же побежит электрический ток, сила которого будет вычисляться по закону Ома I=U/R.

Получается, если через резистор R_AB течет какой-то определенный ток, следовательно, если разложить наш резистор на составляющие R₁ , R₂ , R₃ , то получится, что через них течет та же самая сила тока, которая текла через резистор R_AB .

сила тока через последовательное соединение проводников

Получается, что при последовательном соединении проводников сила тока, которая течет через каждый проводник одинакова. То есть через резистор R₁ течет такая же сила тока, как и через резистор R₂ и такая же сила тока течет через резистор R₃ .

Напряжение при последовательном соединении проводников

Давайте еще раз рассмотрим цепь с тремя резисторами

Как мы уже знаем, при последовательном соединении через каждый резистор проходит одна и та же сила тока. Но вот что будет с напряжением на каждом резисторе и как его найти?

Оказывается, все довольно таки просто. Для этого надо снова вспомнить закон дядюшки Ома и просто вычислить напряжение на  любом резисторе. Давайте так и сделаем.

Пусть у нас будет цепь с такими параметрами.

Мы теперь знаем, что сила тока в такой цепи будет везде одинакова. Но какой ее номинал? Вот в чем загвоздка. Для начала нам надо привести эту цепь к такому виду.

Получается, что в данном случае R_AB =R₁ + R₂ + R₃ = 2+3+5=10 Ом. Отсюда уже находим силу тока по закону Ома I=U/R=10/10=1 Ампер.

Половина дела сделано. Теперь осталось узнать, какое напряжение падает на каждом резисторе. То есть нам надо найти значения U_R1 , U_R2 , U_R3  . Но как это сделать?

Да все также, через закон Ома. Мы знаем, что через каждый резистор проходит сила тока 1 Ампер, мы уже вычислили это значение. Закон ома гласит I=U/R , отсюда получаем, что U=IR.

Следовательно,

U_R1 = IR₁ =1×2=2 Вольта

U_R2 = IR₂ = 1×3=3 Вольта

U_R3 = IR₃ =1×5=5 Вольт

Теперь начинается самое интересное. Если сложить все падения напряжений на резисторах, то можно получить… напряжение источника! Он у нас равен 10 Вольт.

Получается

U=U_R1+U_R2+U_R3

Мы получили самый простой делитель напряжения.

Вывод: сумма падений напряжений при последовательном соединении равняется напряжению питания.

Как определить величину эквивалентного сопротивления при последовательном соединении резисторов

Для последовательного соединения эквивалентное сопротивление равно сумме сопротивлений резисторов, включенных в группу, для расчета применяется формула Rэкв = R₁+R₂+…+Rn.

Например: Нужно посчитать эквивалентное сопротивление данной схемы.

Решение задачи производится путем разделения резистивных элементов на системные группы.

Выделяем первую группу из последовательно соединенных элементов – R₂, R₃, R₄.

Считаем сопротивление Rобщ₁ = R₂+R₃+R₄.

Выделяем вторую группу из последовательных элементов R₁, R₅, R₆.

Считаем сопротивление Rобщ₂ = R₁+R₅+R₆.

Получаем величину двух эквивалентных сопротивлений Rобщ₁ и Rобщ₂, соединенных параллельно.

Делаем расчет всей схемы Rэкв= Rобщ₁× Rобш₂/ (Rобщ₁+ Rобщ₂).

Зная способы соединения и формулы расчета можно рассчитать любую сложную схему соединения резистивных элементов, однако существует множество онлайн калькуляторов, которые сделают это быстрей человека, достаточно только ввести нужные параметры компонентов схемы.

Разница между параллельным и последовательным соединением ламп

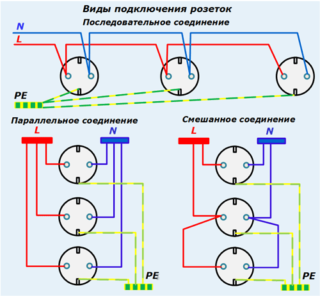
Если любые лампочки включены параллельно друг к другу и соответственно последовательно с выключателем, то напряжение на каждой из них будет равным и таким способом можно соединять источники света разной мощности. Главное условие — это то что рабочее напряжение, при котором они нормально работают, должно быть равно напряжению источника питания. Если в этом случае применяется понижающее устройство с системой выпрямления, то размыкающий контакт должен рассоединять цепь перед преобразователем, как показано на рисунке.

В данном случае несущественно, будет включаться два или три источника света. Чаще всего это галогенные и светодиодные лампы, рассчитанные на пониженное напряжение 12 или же 24 Вольта.

При последовательном соединении ситуация кардинально меняется. Напряжение питания будет разделено на количество лампочек, то есть если сеть 220 Вольт, то на двух подключенных в последовательную цепь, источниках искусственного света, напряжение будет равно примерно 110 Вольт. Это нужно учесть при их выборе и покупке. Ещё один нюанс при таком соединении связан с мощностью каждого из них. Она должна быть одинакова или же максимально близка друг к другу, т.к. при таком соединении ток одинаковый на всех участках цепи. Если одна лампа будет мощностью 500 Вт, а другая 50 Вт, то в лампочке с меньшей мощностью, связанной одним проводом друг с другом, всё равно будет протекать больший ток, соответствующий самой мощной нагрузке. Лампочка с меньшей мощностью мгновенно перегорит. Это правило действуют на все виды источников ламп, от накаливания до светодиодных.

Если нужно подключить с сети или с розеток светодиодный источник света, то зачастую он состоит из так называемого драйвера, устанавливаемого внутри корпуса лампочки. Он выполняет сразу несколько функций: выпрямительную и понижающую. Для последовательного подключения данные осветительные приборы не предназначены, только для параллельного.

Для люминесцентных источников дневного света, как с электронным пусковым устройством, так и со стартером, последовательное подключение встречается чаще всего в растровых светильниках, так как позволяет с помощью одного дросселя и двух стартеров обеспечить стабильную работу. При этом сам стартер выбирается на 127 В с расчётом рабочего напряжения стандартной сети 220 Вольт. Выключатель в этой схеме используется обычный одноклавишный и разрывает своим контактом тоже фазный провод.

Что же касается параллельного подключения нескольких люминесцентных светильников или же компактных ламп, работа которых основана на свечении люминофора, нанесённого на стеклянной трубке, то в этой ситуации можно подключать какое-либо количество к одному выключателю как одноклавишному, так и двухклавишному. Главное, при этом учесть мощность всех источников света, от которой напрямую зависит ток в их цепи. У любого выключателя он ограничен и указан в техническом паспорте, на упаковке или же корпусе. Если, допустим, указан ток 5 А, то превышать его значение не стоит, так как это очень быстро приведёт в негодность сам размыкающий контакт.

Чтобы полностью разобраться с последовательным и параллельным подключением лампочек, рекомендуем просмотреть видео:

Как рассчитать сложные схемы соединения резисторов

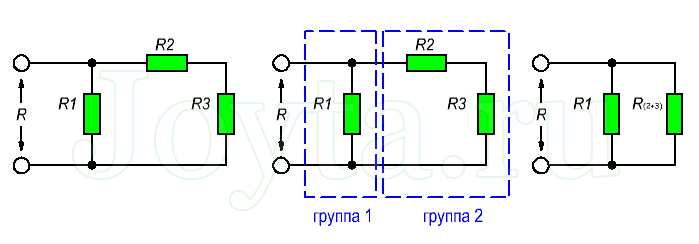
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения. Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Смешанное соединение резисторов

Смешанное соединение резисторов является комбинацией последовательного и параллельного соединения. Иногда подобную комбинацию называют последовательно-параллельным соединением. На рисунке 4 показан простейший пример смешанного соединения резисторов.

Рисунок 4. Смешанное соединение резисторов.

На этом рисунке видно, что резисторы R2 R3 соединены параллельно, а R1, комбинация R2 R3 и R4 последовательно. Для расчета сопротивления таких соединений, всю цепь разбивают на простейшие участки, из параллельно или последовательно соединенных резисторов. Далее следуют следующему алгоритму:1. Определяют эквивалентное сопротивление участков с параллельным соединением резисторов.2. Если эти участки содержат последовательно соединенные резисторы, то сначала вычисляют их сопротивление.3. После расчета эквивалентных сопротивлений резисторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных сопротивлений.4. Рассчитывают сопротивления полученной схемы.

Пример расчета участка цепи со смешанным соединением резисторов приведен на рисунке 5.

Рисунок 5. Расчет сопротивления участка цепи при смешанном соединении резисторов.

Какая мощность тока при последовательном и параллельном соединении

Определение мощности отдельного резистивного элемента производится по формуле

P = U²/R или P = I²R , которую можно вывести из формулы расчета мощности электрической цепи P = UI по закону Ома.

Мощность при параллельном соединении

Рассчитав сопротивление каждого элемента в отдельности, считаем мощность каждого по формуле P = I²R, где

• R – не номинальное сопротивление резистивного элемента, а рассчитанное для данной цепи;
• I – сила тока в цепи.

При параллельном соединении через меньший резистор протекает больший ток – мощность рассеивания на этом резистивном элементе будет больше, чем на остальных.

Мощность при последовательном соединении

Вычислив сопротивление каждого резистивного элемента по отдельности, рассчитываем мощность каждого по формуле P = U²/R, где

• R – рассчитанное нами сопротивление для определенной схемы;
• U – падение напряжения на данном резистивном элементе.

Вопросы на параллельное и последовательное соединение проводников

Вопрос 1. Схематически изобразите последовательное соединение проводников

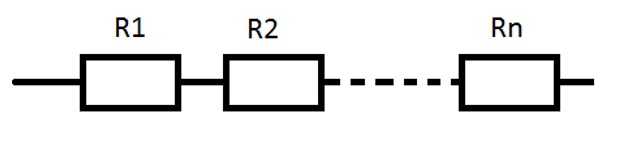
Ответ. На рисунке ниже изображен участок цепи с последовательно соединенными проводниками:

Вопрос 2. Схематически изобразите параллельное соединение проводников

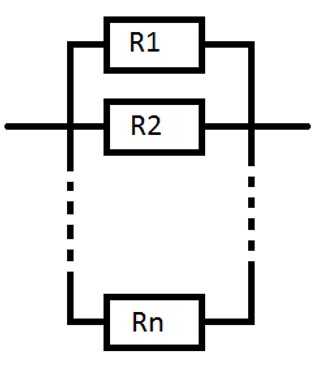
Ответ. На рисунке ниже изображено параллельное соединение проводников:

Вопрос 3. Приведите основные формулы и соотношения для последовательного соединения проводников.

Ответ. При последовательном соединении:

1. Сила тока во всех проводниках одинакова.
2. Общее напряжение равно сумме напряжений на каждом проводнике.
3. Полное сопротивление цепи равно сумме сопротивлений отдельных проводников.

Вопрос 4. Приведите основные формулы и соотношения для параллельного соединения проводников.

Ответ. Для параллельного соединения проводников:

1. Напряжение на всех проводниках одинаково.
2. Сила тока в неразветвленной цепи равна сумме токов в параллельно соединенных проводниках.
3. Величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

Вопрос 5. Какие электрические цепи нельзя рассчитать с помощью формул для последовательного и параллельного соединения проводников?

Ответ. С помощью приведенных выше формул можно рассчитать лишь относительно простые электрические цепи. Для расчета сложных цепей, включающих в себя несколько источников тока и состоящих из многих резисторов, применяются правила Кирхгофа.

Нужна помощь в решении задач или любых других учебных заданий? Обращайтесь в профессиональный сервис для учащихся: мы найдем верное решение.

Какая мощность тока при последовательном и параллельном соединении

Определение мощности отдельного резистивного элемента производится по формуле

P = U²/R или P = I²R , которую можно вывести из формулы расчета мощности электрической цепи P = UI по закону Ома.

Мощность при параллельном соединении

Рассчитав сопротивление каждого элемента в отдельности, считаем мощность каждого по формуле P = I²R, где

• R – не номинальное сопротивление резистивного элемента, а рассчитанное для данной цепи;
• I – сила тока в цепи.

При параллельном соединении через меньший резистор протекает больший ток – мощность рассеивания на этом резистивном элементе будет больше, чем на остальных.

Мощность при последовательном соединении

Вычислив сопротивление каждого резистивного элемента по отдельности, рассчитываем мощность каждого по формуле P = U²/R, где

• R – рассчитанное нами сопротивление для определенной схемы;
• U – падение напряжения на данном резистивном элементе.

Последовательное соединение резисторов.

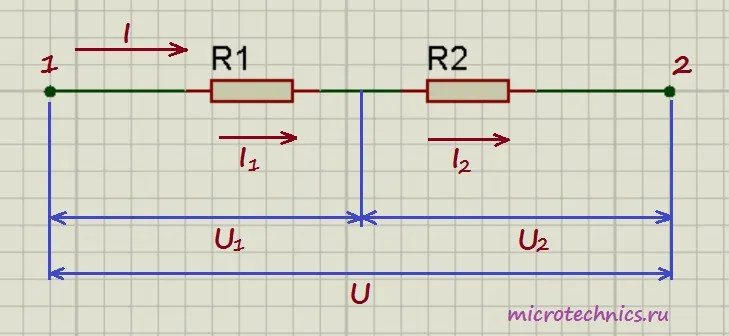
Давайте начнем с рассмотрения цепей, элементы которой соединены последовательно. И хоть мы и будем рассматривать только резисторы в качестве элементов цепи в данной статье, но правила, касающиеся напряжений и токов при разных соединениях будут справедливы и для других элементов. Итак, первая цепь, которую мы будем разбирать выглядит следующим образом:

Здесь у нас классический случай последовательного соединения – два последовательно включенных резистора. Но не будем забегать вперед и рассчитывать общее сопротивление цепи, а для начала рассмотрим все напряжения и токи. Итак, первое правило заключается в том, что протекающие по всем проводникам токи при последовательном соединении равны между собой:

I = I_1 = I_2

А для определения общего напряжения при последовательном соединении, напряжения на отдельных элементах необходимо просуммировать:

U = U_1 + U_2

В то же время, по закону Ома для напряжений, сопротивлений и токов в данной цепи справедливы следующие соотношения:

U_1 = I_1R_1 = IR_1
U_2 = I_2R_2 = IR_2

Тогда для вычисления общего напряжения можно будет использовать следующее выражение:

U = U_1 + U_2 = IR_2 + IR_2 = I(R_1 + R_2)

Но для общего напряжение также справедлив закон Ома:

U = IR_0

Здесь R_0 – это общее сопротивление цепи, которое исходя из двух формул для общего напряжения равно:

R_0 = R_1 + R_2

Таким образом, при последовательном соединении резисторов общее сопротивление цепи будет равно сумме сопротивлений всех проводников.

Например для следующей цепи:

Общее сопротивление будет равно:

R_0 = R_1 + R_2 + R_3 + R_4 + R_5 + R_6 + R_7 + R_8 + R_9 + R_{10}

Количество элементов значения не имеет, правило, по которому мы определяем общее сопротивление будем работать в любом случае А если при последовательном  соединении все сопротивления равны (R_1 = R_2 = … = R), то общее сопротивление цепи составит:

R_0 = nR

В данной формуле n равно количеству элементов цепи. С последовательным соединением резисторов мы разобрались, давайте перейдем к параллельному.

Как рассчитать сложные схемы соединения резисторов

Сложные схемы рассчитываются путем группировки по параллельному и последовательному способу соединения.

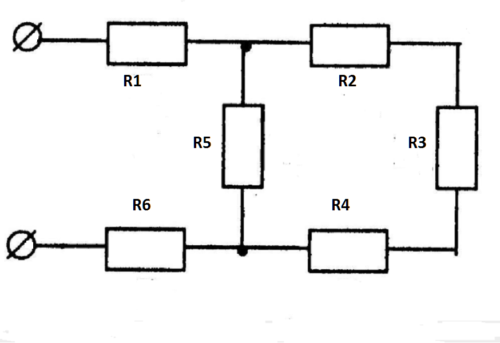
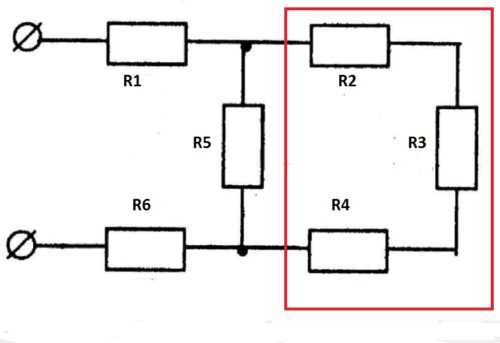
Перед нами сложная схема – задача рассчитать общее сопротивление:

1. R₂, R₃, R₄ объединим в последовательную группу – применим формулу R_2,3,4 = R₂+R₃+_R4.
2. R₅ и R_2,3,4 – параллельно соединенные резисторы, рассчитаем R_5,2,3,4 = 1/ (1/R₅+1/R_2,3,4).
3. R_5,2,3,4, R₁, R₆ опять объединяем в последовательную группу – суммируя величины, получаем Rобщ = R_5,2,3,4+R₁+R₆.

Для больших схем существуют специальные методы, облегчающие расчет. Один из таких методов – эквивалентное преобразование «треугольника» в «звезду». Такая система расчета применяется в том случае, когда невозможно по схеме определить последовательное или параллельное подключение резисторов.

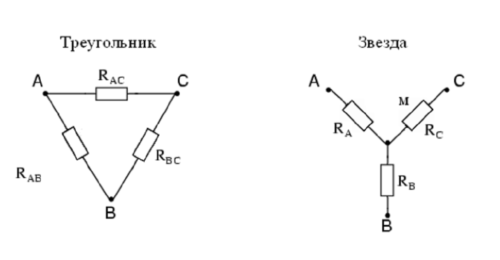
Преобразование «звезда-треугольник»

Для соединения резистивных элементов, кроме вышеописанных способов, существует несколько других видов соединения:

• «звезда» – соединение трех ветвей с одним общим узлом;
• «треугольник» – соединение ветвей схемы в виде треугольника, сторонами которого служат ветви, вершины представляют узлы.

Эквивалентность замены предполагает стабильность токов, входящих в каждый узел, при одинаковых напряжения между одноименными узлами «треугольника» и «звезды».

Сопротивление резистора луча «звезды» равно произведению сопротивлений резисторов прилегающих сторон «треугольника», деленному на сумму сопротивлений резисторов трех сторон «треугольника».

R_A = R_AB R_AC/(R_AB+R_AC+R_DC).

Сопротивление резисторов сторон «треугольника» равно сумме произведения сопротивлений резисторов двух прилегающих лучей «звезды», деленного на сопротивление третьего луча.

R_AB=(R_AR_B+R_AR_C+R_BR_С)/R_C

О разнице подключения звезда и треугольник читайте здесь.

Последовательное соединение резисторов

Основная функция резисторов состоит в ограничении и регулировке тока, с помощью которых создаются необходимые падения напряжения на определенных участках цепей. Кроме того, резисторы осуществляют фильтрацию тока и напряжения, позволяя устанавливать заданные параметры в устройствах и приборах. Их подключение к цепи может производиться различными способами. Одним из них является последовательное соединение резисторов, с целью создания на конкретном участке определенного сопротивления.

Схема последовательного соединения

Данная схема предполагает соединение конца первого резистора и начала второго. В свою очередь, второй резистор своим концом соединяется с началом следующего. Это подключение повторяется до того момента, пока не будут получены необходимые показатели в цепи.

При последовательном соединении все элементы пропускают через себя одинаковый ток. Ранее, роль резисторов выполняли электронные лампы. При одном и том же значении тока, можно сделать вывод, что общее сопротивление последовательно соединенной цепи представляет собой сумму сопротивлений, находящихся в ней резисторов.

То же самое касается и напряжения. Его значение на клеммах источника тока состоит из суммы напряжений всех резисторов, включенных в последовательную цепь. Причем, величина напряжения каждого резистора находится в пропорциональной зависимости от его сопротивления. Таким образом, при увеличении сопротивления одного из элементов цепи, наблюдается рост напряжения, приложенного к нему.

Практическая работа последовательного соединения

Основным свойством последовательно соединенных приемников является изменяющееся напряжение в случае изменения их сопротивления. Даже если сопротивление изменится хотя бы в одном из них, то напряжение будет изменяться и в других приемниках, соединенных с ним.

В случае обрыва или отключения электрической цепи в каком-либо резисторе, прохождение тока прекращается и в других приемниках. В связи с этим, последовательное соединение резисторов используется довольно редко, только тогда, когда напряжение источника значительно превышает расчетное напряжение потребителя. Например, если напряжение источника тока составляет 1000 ватт, то для нормальной работы необходимо последовательно включить 10 лампочек по 100 ватт каждая.

Таким образом, данный вид соединения обеспечивает нормальную работу цепей в определенных ситуациях. В других случаях могут применяться параллельное или смешанное подключение резисторов.

Правила параллельного соединения, схема

Все устройства, которые соединены параллельно или последовательно, функционируют по собственным правилам. Они базируются на основных законах электротехники и некоторых тонкостях.

Порой эти тонкости не являются очевидными для тех, кто мало разбирается в теме. Работая с той или иной схемой подключения, нужно учитывать:

• для последовательного соединения характерны одинаковые показатели тока на всех участках;
• в каждом конкретном виде соединений закон Ома приобретает собственное значение — в последовательном подключении напряжение соответствует напряжению на всех частях цепи;
• при параллельном соединении напряжение отдельных участков цепи не складывается — оно одинаково везде;
• сила тока при соединении параллельного типа соответствует общей силе тока всех ветвей цепи.

Удачи в подключении!

Отличия от последовательного и смешанного подключений

Иные способы соединения понятны из показанных на картинке примеров. Без специальных вычислений понятно, что параллельное включение резисторов создает несколько путей прохождения тока. Следовательно, в отдельных цепях его сила будет меньше, по сравнению с контрольными точками на входе и выходе. Вместе с тем напряжение в отмеченных местах остается неизменным.

Последовательное соединение резисторов увеличивает общее электрическое сопротивление. Ток в этой цепи (по базовым принципам) не будет изменяться. Однако на каждом пассивном элементе можно будет обнаружить измерительным прибором соответствующее падение напряжения.

Смешанный вариант – это объединение представленных выше соединений. Различные комбинации используют для деления напряжения, решения других задач. Для упрощения расчетов суммируют последовательность соединенных сопротивлений в отдельных цепях:

Rобщ = R1 + R2 + … + Rn.

Вне зависимости от сложности схемы, на входе и выходе по первому закону Кирхгофа токи будут одинаковыми.

Смешанное соединение резисторов.

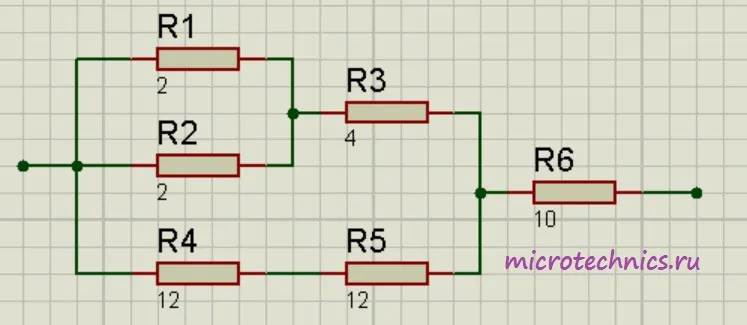
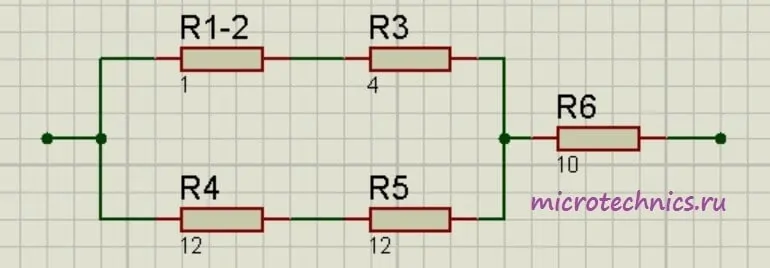
Помимо параллельного и последовательного соединений резисторов существует еще смешанное соединение. Из названия уже понятно, что при таком соединении в цепи присутствуют резисторы, соединенные как параллельно, так и последовательно. Вот пример такой цепи:

Давайте рассчитаем общее сопротивление цепи. Начнем с резисторов R_1 и R_2 – они соединены параллельно. Мы можем рассчитать общее сопротивление для этих резисторов и заменить их в схеме одним единственным резистором R_{1-2}:

R_{1-2} = \frac{R1\cdot R2}{R1 + R2} = 1

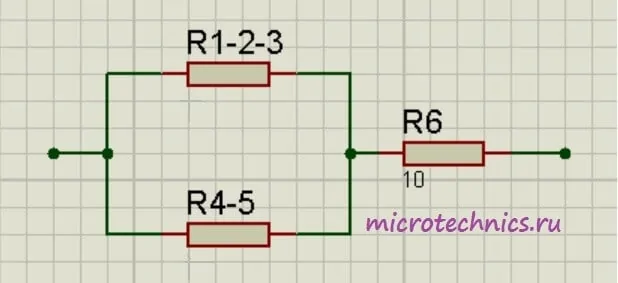
Теперь у нас образовались две группы последовательно соединенных резисторов:

• R_{1-2} и R_3
• R_4 и R_5

Заменим эти две группы двумя резисторами, сопротивление которых равно:

R_{1-2-3} = R_{1-2} + R_3 = 5
R_{4-5} = R_4 + R_5 = 24

Как видите, схема стала уже совсем простой Заменим группу параллельно соединенных резисторов R_{1-2-3} и R_{4-5}  одним резистором R_{1-2-3-4-5}:

R_{1-2-3-4-5}\enspace = \frac{R_{1-2-3}\medspace\cdot R_{4-5}}{R_{1-2-3} + R_{4-5}} = \frac{5\cdot24}{5 + 24} = 4.14

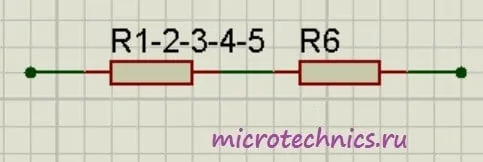
И в итоге у нас на схеме осталось только два резистора соединенных последовательно:

Общее сопротивление цепи получилось равным:

R_0 = R_{1-2-3-4-5}\medspace +\medspace R_6 = 4.14 + 10 = 14.14

Таким вот образом достаточно большая схема свелась к простейшему последовательному соединению двух резисторов!

Тут стоит отметить, что некоторые схемы невозможно так просто преобразовать и определить общее сопротивление – для таких схем нужно использовать правила Кирхгофа, о которых мы обязательно поговорим в будущих статьях. А сегодняшняя статья на этом подошла к концу, до скорых встреч на нашем сайте!

Основы РЕМОНТА

Отдельные участки цепи.

Наличие сопротивления в электрической цепи в большинстве случаев нежелательно. Однако в ряде устройств, наоборот, необходимо, чтобы отдельные участки цепи обладали определенным сопротивлением, что обычно достигается с помощью резисторов.

Резисторы являются широко распространенными элементами современной радиоэлектронной аппаратуры. Они бывают проволочными и не проволочными, у последних в качестве проводящего слоя используется углеродистый или другой специальный состав, нанесенный на поверхность цилиндрических каркасов из изоляционного материала.

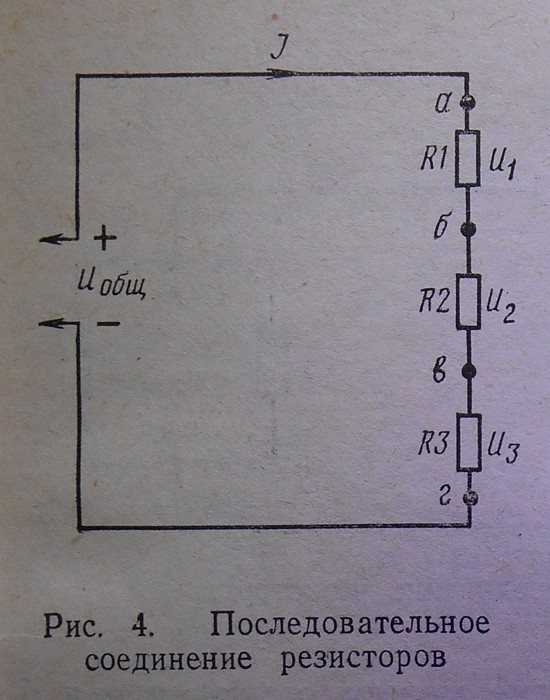
Если несколько резисторов соединить так, чтобы конец одного был соединен с началом другого, как это показано на рис. 4, то получится последовательное их соединение. Такое включение резисторов равносильно удлинению провода, а это, как известно, приводит к увеличению общего сопротивления. При последовательном соединении резисторов общее сопротивление цепи R общ равняется сумме сопротивлений всех включенных в цепь резисторов, т. е. R общ — Rl + R2 + R3. Сила тока в цепи, состоящей из последовательно соединенных резисторов, одинакова на любом участке этой цепи, таккак ток последовательно проходит через все резисторы.Применяя закон Ома к схеме, изображенной на рис. 4, найдем, что напряжение между точками а и б U1 = IR1 напряжение между точками б и в U2 = IR2 и, наконец, напряжение между точками в и г U3 = IR3.

Сумма напряжений U1 + U2 + U3 равна напряжению на клеммах источника тока (U0бщ).

Таким образом, в цепи с последовательно соединенными резисторами падение напряжения на каждом из них пропорционально величине их сопротивлений,

а суммарное падение напряжения на всех резисторах равно напряжению на зажимах источника.

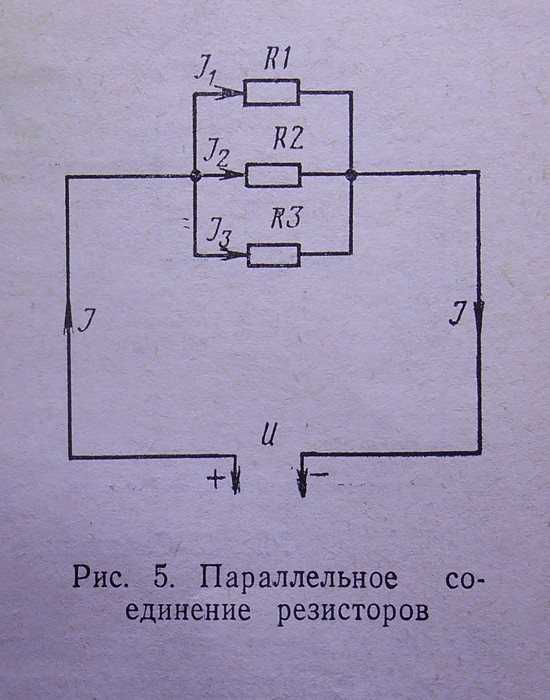
Другой способ соединения резисторов, при котором их начала так же, как и концы, соединяются вместе, называемый параллельным соединением, показан на рис. 5.

При таком соединении общее сопротивление цепи оказывается меньше самого малого сопротивления, которым обладает один из включенных резисторов.

Для определения общего или эквивалентного сопротивления при параллельном соединении резисторов исходят из того, что общая проводимость цепи равна в этом случае сумме проводимостей отдельных ее ветвей, т. е.

Gобщ = G1 + G2 + G3

ИЛИ

Из последнего уравнения и находят общее сопротивление цепи.

При параллельном включении резисторов ток от источника разветвляется, проходя по каждой из параллельных ветвей. При этом

общая сила тока в цепи равна сумме сил токов, проходящих по каждому параллельно включенному резистору, т. е. Iо6их = I1 + I2 + I3 .

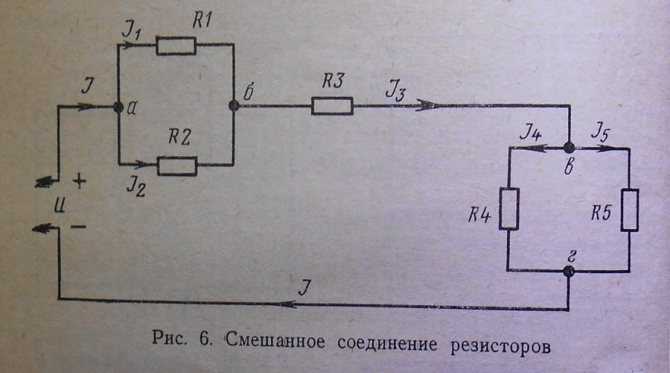
Кроме последовательного и параллельного соединений, в практике часто используется так называемое смешанное соединение резисторов, когда часть их включена последовательно, а другая часть — параллельно (рис. 6).

Для того чтобы найти общее сопротивление такой цепи, сначала определяют эквивалентные сопротивления участков цепи с параллельным соединением резисторов (Ra6 и Rвг), а затем находят общее сопротивление:

Rобщ = Rаб + R3 + Rвг .

Метки: резисторы, соединение резисторов

Заработай на кэшбэке делясь товаром Вперед

Типы проводников

Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.

Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:

1. Проводники (все металлы, ионизированный газ и электролитические растворы).
2. Полупроводники (Si, Ge, GaAs, InP и InSb).
3. Непроводники (диэлектрики или изоляторы).

Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.

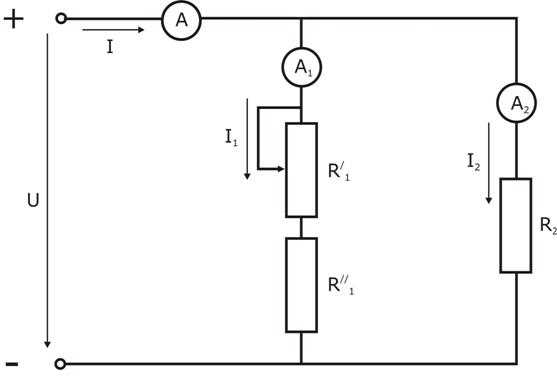
4.3. Параллельное соединение. Опыт №2

На стенде собрана цепь по схеме рис. 4.2.

Рис. 4.2. Схема проведения опыта №2

1. Рукоятку соответствующего параллельному соединению
ЛАТРа установите в нулевое положение, потенциометр  полностью
введен.

2. Нажмите на кнопку подачи постоянного напряжения
соответствующего источника питания.

3. Установите напряжение  В
и снимите показания всех приборов.

4. Данные занесите в таблицу 4.2.

Примечание: ;
.

Таблица 4.2

Измерено	Вычислено
, В	, А	, А	, А	, Ом	, Ом	, Ом	, Вт	, Вт	, Вт

5. Не меняя напряжение источника питания  В,
нужно полностью вывести потенциометр .
Результаты всех приборов занесите таблицу 4.2.

6. Рассчитайте величины, входящие в таблицу 4.2.

Последовательное соединение резисторов.

Последовательным называют соединение, при котором резисторы следуют друг за другом и образуют электрическую цепь из нескольких элементов, в которой конец одного резистора соединен с началом другого и т.д.

В последовательной цепи электрической ток поочередно протекает по всем резисторам и преодолевает сопротивление каждого из них. При этом ток в этой цепи одинаков. И если последовательно соединить два резистора R1 и R2, их общее (полное) сопротивление Rобщ будет равно сумме их сопротивлений. Это условие справедливо для любого числа резисторов, где:

Например.При соединении двух резисторов с номиналами R1 = 150 Ом и R2 = 330 Ом их общее сопротивление составит Rобщ = 150 + 330 = 480 Ом.

При соединении трех резисторов R1 = 20 кОм, R2 = 68 кОм и R3 = 180 кОм их общее сопротивление составит Rобщ = 20 + 68 + 180 = 268 кОм.

Запомните. Из нескольких соединенных последовательно резисторов их общее сопротивление Rобщ определяет тот, у которого сопротивление больше по отношению к другим резисторам в этой цепи.

Смешанное подключение

При смешанном подключении в одной схеме сочетаются несколько видов соединений – последовательное, параллельное соединение резисторов и их комбинации. Самую сложную электрическую схему, состоящую из источников питания, диодов, транзисторов, конденсаторов и других радиоэлектронных элементов можно заменить резисторами и источниками напряжения, параметры которых изменяются в каждый момент времени. О параллельном соединении резистора и конденсатора читайте тут.

Смешанная схема делится на фрагменты, ток и напряжение рассчитывается для каждого отдельно в зависимости от того, как они соединены на выбранном сегменте электрической схемы.

Последовательное соединение

Последовательная схема подключения предполагает расположение резисторов в схеме таким образом, что конец первого элемента соединяется с началом второго, а конец второго – с началом третьего и т.д. То есть все резисторы поочередно следуют друг за другом. Сила тока при последовательном соединении будет одинаковой в каждом элементе. В виде формулы это выглядит следующим образом: Iобщ = I1 = I2, где Iобщ является общим током цепи, I1 и I2 – соответствуют токам 1-го и 2-го резистора.

В соответствии с законом Ома, напряжение источника питания будет равно сумме падений напряжения на каждом резисторе: Uобщ = U1 + U2 = I1r1 + I2r2, в которой Uобщ – напряжение источника электроэнергии или самой сети; U1 и U2 – значение падений напряжения на 1-м и 2-м резисторах; r1 и r2 – сопротивления 1-го и 2-го резисторов. Поскольку токи на любом участке цепи имеют одинаковое значение, формула приобретает вид: Uобщ = I(r1 + r2).

Таким образом, можно сделать вывод, что при последовательной схеме включения резисторов, электрический ток, протекающий через каждый из них равен общему значению тока во всей цепи. Напряжение на каждом резисторе будет разное, однако их общая сумма составит значение, равное общему напряжению всей электрической цепи. Общее сопротивление цепи также будет равно сумме сопротивлений каждого резистора, включенного в эту цепь.

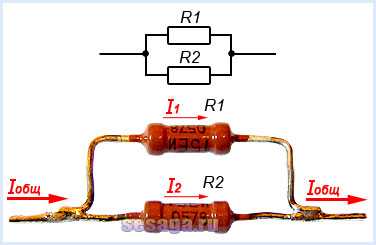
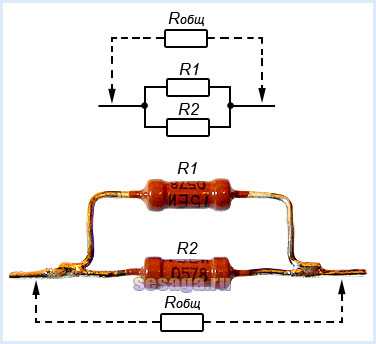
Параллельное соединение резисторов

При параллельном соединении резисторов соединяются их одноименные выводы: начальные выводы соединяются в одной точке, а конечные выводы в другой. Такой способ включения облегчает прохождение электрическому току, потому что он разветвляясь, одновременно протекает по всем соединенным таким образом резисторам.

При параллельном соединении резисторов складываются не сопротивления, а их электрические проводимости (величины, обратные сопротивлениям, т.е. 1/R), поэтому общее (полное) сопротивление Rобщ уменьшается и всегда меньше сопротивлений любого резистора в этой цепи. Формула для определения полного сопротивления имеет вид:

Если параллельно включены два резистора с сопротивлениями R1 и R2, тогда основную формулу немного упрощаем и получаем:

При включении трех резисторов расчет общего сопротивления будет таким:

Например.При соединении двух резисторов с номиналами R1 = 47 кОм и R2 = 68 кОм их общее сопротивление составит Rобщ = 47•68 / (47 + 68) = 27,8 кОм.

При соединении трех резисторов R1 = 10 Ом, R2 = 15 Ом и R3 = 33 Ом их общее сопротивление равно Rобщ = 10•15•33 / (15•33) + (10•33) + (10•15) = 5,07 Ом.

На заметку. При соединении двух резисторов с одинаковыми номиналами их общее сопротивление Rобщ равно половине сопротивления каждого из них.

Из приведенных примеров можно сделать вывод, что если необходим резистор с большим сопротивлением, применяют последовательное соединение. Если же резистор необходим с меньшим сопротивлением, применяют параллельное соединение.

Ну вот, в принципе, и все, что хотел сказать о последовательном и параллельном соединении резисторов. И в дополнение к статье предлагаю еще рассмотреть и смешанное соединение.
Удачи!