Алгебра логики

Гомоморфизмы и изоморфизмы

Гомоморфизм между двумя булевыми алгебрами A и B является функцией F  : → B , что для всех а , б , в A

f ( a ∨ b ) = f ( a ) ∨ f ( b ),

f ( a ∧ b ) = f ( a ) ∧ f ( b ),

f (0) = 0,

f (1) = 1.

Из этого следует , что п (¬ ) = ¬ е ( ) для всех а в А . Класс всех булевых алгебр, вместе с этим понятием морфизма, образует полную подкатегорию в категории решеток.

Изоморфизм между двумя булевыми алгебрами A и B есть гомоморфизм F  : → B с обратным гомоморфизмом, то есть гомоморфизм гB → A такой , что композиция г ∘ е : → является функцией тождества на А , и композиция F ∘ гB → B является функцией тождественный на B . Гомоморфизм булевых алгебр является изоморфизмом тогда и только тогда, когда он биективен .

История

Термин «булева алгебра» чтит Джорджа Буля (1815–1864), английского математика-самоучки. Первоначально он представил алгебраическую систему в небольшой брошюре «Математический анализ логики» , опубликованной в 1847 году в ответ на продолжающийся общественный спор между Августом Де Морганом и Уильямом Гамильтоном , а затем в более содержательной книге «Законы мысли» , опубликованной в 1854. Формулировка Буля отличается от описанной выше в некоторых важных отношениях. Например, конъюнкция и дизъюнкция в логическом выражении не были парными операциями. Булева алгебра появилась в 1860-х годах в статьях, написанных Уильямом Джевонсом и Чарльзом Сандерсом Пирсом . Первое систематическое представление булевой алгебры и дистрибутивных решеток причитается 1890 Vorlesungen от Эрнста Шрёдера . Первое обширное исследование булевой алгебры на английском языке — это Универсальная алгебра А. Н. Уайтхеда 1898 года . Булева алгебра как аксиоматическая алгебраическая структура в современном аксиоматическом смысле начинается со статьи Эдварда В. Хантингтона 1904 года . Булева алгебра достигла зрелости как серьезная математика с работами Маршалла Стоуна в 1930-х годах и с Теорией решеток Гаррета Биркгофа 1940 года . В 1960-х годах Пол Коэн , Дана Скотт и другие нашли глубокие новые результаты в математической логике и аксиоматической теории множеств, используя ответвления булевой алгебры, а именно модели с принуждением и булевозначные модели .

Операции булевой алгебры

Мы уже помним, что операции в алгебре суждений – логические. Подобно тому, как алгебра чисел использует арифметические операции для сложения, вычитания или сравнения чисел, элементы математической логики позволяют составить сложные высказывания, дать отрицание или вычислить конечный результат.

Логические операции для формализации и простоты записываются формулами, привычными для нас в арифметике. Свойства булевой алгебры дают возможность записывать уравнения и вычислять неизвестные. Логические операции обычно записывают с помощью таблицы истинности. Её столбцы определяют элементы вычислений и операцию, которая над ними производится, а строки показывают результат вычислений.

Построение формулы логической функции по таблице истинности

Строится формула следующим образом:

• В таблице истинности выделяются строки, в которых значение функции истинно.
• Для каждой такой строки таблицы записывается конъюнкция всех переменных следующим образом: если значение переменной истинно, то она записывется в прямом виде, а если ложно, то — с инверсией.
• Все, таким образом полученные, конъюнкции объединяются дизъюнкцией

В форме записи выражения логической функции, полученной таким образом,  не содержатся отрицания неэлементарных формул и присутствуют только основные логические операции (отрицание, конъюнкция, дизъюнкция). Такая форма логической функции называется дизъюнктивной нормальной формой

Если все конъюнкции в выражении состоят из одного и того же набора переменных, каждый из которых входит в конъюнкцию один раз, то такая форма называется совершенной дизъюнктивной нормальной формой.

Задача: Дана полная таблица истинности некоторой функции. Построить формулу функции по этой таблице.

\( x \)	\( y \)	\( z \)	\( F \)
1
1	1
1	1
1	1
1	1	1
1	1
1	1	1	1

 1. Удаляем строки со значением функции равным 0

\( x \)	\( y \)	\( z \)	\( F \)
1	1
1	1
1	1	1
1	1	1	1

2. Составляем конъюнкции для каждой строки

\( x \)	\( y \)	\( z \)	\( F \)	Конъюнкция
1	1	\( \overline{x} ⋅ y ⋅ \overline{z} \)
1	1	\( x ⋅ \overline{y} ⋅ \overline{z} \)
1	1	1	\( x ⋅ \overline{y} ⋅ z \)
1	1	1	1	\( x ⋅ y ⋅ z \)

3. Объединяем все конъюнкции дизъюнкцией:

\( F(x,y,z) = \overline{x} ⋅ y ⋅ \overline{z} + x ⋅ \overline{y} ⋅ \overline{z} + x ⋅ \overline{y} ⋅ z + x ⋅ y ⋅ z \)

Закон исключенного третьего.

Это — один из законов поглощения:

x ~x = 1

В булевой алгебре этот закон оспорить невозможно, так
как достаточно подставить значения x = 0, 1
и убедиться в наличии равенства в обоих случаях. Применение
этого закона на практике, например в психологике, накладывает
дополнительные ограничения, описанные
в первой главе. Что, впрочем,
справедливо и для осталных законов булевой алгебры.

Я специально останавливаюсь на этом законе потому, что в
некоторых логических системах (интуиционистская логика,
конструктивная логика), которые построены на иных
принципах, чем булева алгебра, в этих системах закон
исключенного третьего не действует. Что
неудивительно, ведь в тех системах совсем другие границы применимости.

Представление булевых функций через конъюнкцию, дизъюнкцию и отрицание

Теорема 10.5 (о представлении булевых функций через конъюнкцию, дизъюнкцию и отрицание). Всякая булева функция может быть представлена в виде суперпозиции конъюнкции, дизъюнкции и отрицания; причем знак отрицания стоит только непосредственно около переменной и не стоит ни перед одной из внутренних скобок.

Доказательство будем вести методом математической индукции по числу аргументов функции .

В предыдущем параграфе перечислены все булевы функции от одного аргумента. Их всего четыре. Напомним их (используя равенства теоремы 9.3, пункт и):

Отсюда видно, что все функции от одного аргумента выражаются через конъюнкцию, дизъюнкцию и отрицание; причем знак отрицания стоит только непосредственно около переменных. Это означает, что утверждение теоремы справедливо при .

Предположим, что теорема верна для всех функций от аргументов. Докажем ее для функций от аргумента. Пусть — произвольная булева функция от аргумента. На основании предыдущей леммы запишем разложение данной функции по последней переменной:

Как отмечалось в начале настоящего параграфа, фиксирование в булевой функции одного аргумента приводит к булевой функции с числом аргументов на единицу меньшим, нежели число аргументов исходной функции. Так что каждая из функций и есть булева функция от аргументов. Но согласно предположению индукции, все такие функции выражаются через конъюнкцию, дизъюнкцию и отрицание, причем знак отрицания стоит только непосредственно около переменных и не стоит ни перед одной из внутренних скобок

Принимая это во внимание, видим, что правая часть последнего равенства представляет собой суперпозицию лишь трех функций — конъюнкции, дизъюнкции и отрицания. Причем отрицание стоит около переменной

Это и доказывает окончательно теорему.

Логические функции

Логические функции одной переменной

Функция	Название	Обозначение
	Константа нуля
	Повторение x
	Логическое отрицание, инверсия, «НЕ»
	Константа единицы

Переменная	Логические функции
x
1	1
1	1	1

Логические функции двух переменных

Функция	Название	Обозначение
	Константа нуля	или False
	Логическое умножение, конъюнкция, «И»	или или или
	Запрет по	или
	Переменная
	Запрет по	или
	Переменная
	Сложение по модулю 2, отрицание эквивалентности, исключающее «ИЛИ»	или или
	Логическое сложение, дизъюнкция, «ИЛИ»	или или или
	Функция Пирса (Вебба), «ИЛИ-НЕ»	или или
	Логическая равнозначность, эквиваленция	или или или
	Отрицание
	Правая импликация	или
	Отрицание
	Левая импликация	или
	Функция Шеффера, «И-НЕ»	или или
	Константа единицы	или True

Ниже дана таблица истинности для логических функций от двух переменных.

X1	1	1
X2	1	1
	1
	1
	1	1
	1
	1	1
	1	1
	1	1	1
	1
	1	1
	1	1
	1	1	1
	1	1
	1	1	1
	1	1	1
	1	1	1	1

В логических схемах функции могут быть реализованы с произвольных количеством
входных переменных, примеры — в материале Логические схемы и таблицы истинности.

Ответить на контрольные вопросы, а затем посмотреть ответы

Контрольный вопрос 1. Даны две переменные
и .
Число различных булевых векторов и различных ФАЛ от полученных векторов равны соответственно:

• 8 и 16
• 8 и 32
• 4 и 8
• 4 и 16

Контрольный вопрос 2. Какие из функций не являются ФАЛ одной переменной
(и одна, и вторая в варианте ответа):

• отрицание и сложение по модулю два
• эквивалентность и повторение
• отрицание и импликация
• функция Шеффера и эквивалентность
• запрет по и отрицание

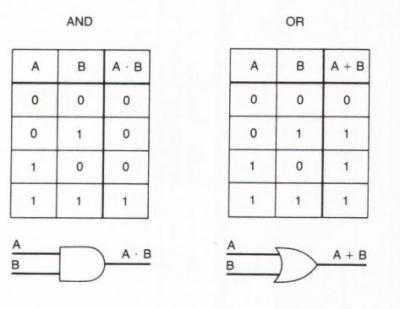
Логические умножение и сложение

Логическое И называют операцией конъюнкции. Что это значит? Во-первых, что применить ее можно к двум операндам, т. е. И – бинарная операция. Во-вторых, что только в случае истинности обоих операндов (и А, и Б) истинно и само выражение. Пословица «Терпение и труд все перетрут» предполагает, что только оба фактора помогут человеку справиться со сложностями.

Для записи используются символы: A∧Б, A⋅Б или A&&Б.

Конъюнкция аналогична умножению в арифметике. Иногда так и говорят – логическое умножение. Если перемножить элементы таблицы по строкам, мы получим результат, аналогичный логическому размышлению.

Дизъюнкцией называют операцию логического ИЛИ. Она принимает значение истинности тогда, когда хотя бы одно из высказываний истинно (или А, или Б). Записывается это так: A∨Б, A+Б или A||Б. Таблицы истинности для этих операций такие:

Дизъюнкция подобна арифметическому сложению. Операция логического сложения имеет только одно ограничение: 1+1=1. Но мы же помним, что в цифровом формате математическая логика ограничена 0 и 1 (где 1 – истина, 0 — ложь). Например, утверждение «в музее можно увидеть шедевр или встретить интересного собеседника» означает, что можно посмотреть произведения искусства, а можно познакомиться с интересным человеком. В то же время, не исключен вариант одновременного свершения обоих событий.

Изоморфность булевой алгебры прямому произведению двух булевых алгебр

В силу доказанных теорем имеем следующий результат.

Следствие 4.2. Любая булева алгебра изоморфна прямому произведению некоторых двух булевых алгебр.

На рис. 4.4 представлены все возможные способы представления четырехэлементной булевой алгебры (ее элементы обозначены ) в виде прямого произведения двух двухэлементных булевых алгебр. Эти представления определяются изоморфизмами и . Изоморфизм есть изоморфизм исходной четырехэлементной булевой алгебры на декартово произведение ее отрезков и , каждый из которых изоморфен двухэлементной булевой алгебре . Вместе с тем декартово произведение указанных отрезков дает четырехэлементную булеву алгебру, элементами которой служат упорядоченные пары и , причем пара будет нулем, а пара — единицей этой булевой алгебры, которая изоморфна исходной. Аналогично рассматривается изоморфизм .

Интересно отметить, что могут быть заданы и изоморфизмы и , но каждый из них определяет тривиальное разложение исходной булевой алгебры в виде ее прямого произведения на одноэлементную булеву алгебру, т.е. в виде или в виде . Интерес представляют, следовательно, такие изоморфизмы , где элемент не является ни нулем, ни единицей исходной булевой алгебры.

Теперь, наконец, мы докажем основной результат.

Теорема 4.15. Любая конечная булева алгебра изоморфна булевой алгебре для некоторого .

Доказательство проведем методом математической индукции по числу элементов булевой алгебры . Одноэлементная булева алгебра изоморфна нулевой степени алгебры (см. замечание 4.4). Для самой алгебры , содержащей два элемента, доказывать нечего.

Пусть утверждение теоремы доказано для всех булевых алгебр с числом элементов, не большим некоторого . Рассмотрим произвольную булеву алгебру , содержащую элемент, т.е. , и пусть . Поскольку число элементов в данной алгебре не меньше трех, то, во-первых, (нуль совпадает с единицей только в одноэлементной булевой алгебре), а во-вторых, можно выбрать элемент так, что (т.е. отлично и от нуля и от единицы).

Тогда по теореме 4.14 . Так как элемент а отличен от единицы алгебры , то отрезок не содержит единицы , а так как , то отрезок не содержит нуля алгебры . Следовательно, число элементов в каждом из отрезков не превышает .

В соответствии с предположением индукции найдутся такие неотрицательные целые числа и , что , а . Поэтому .

Следствие 4.3. Мощность конечной булевой алгебры есть некоторая степень двойки.

(помощь с решением задач, обсуждение вопросов по математике).

Определение

Определение «Определение — Алгебра логики (булева алгебра)’»
Алгебра логики (булева алгебра) — это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними. Алгебра логики позволяет закодировать любые утверждения, истинность или ложность которых нужно доказать, а затем манипулировать ими подобно обычным числам в математике.

Булева алгебра как предметная область определяется следующими критериями:

1. Непустое множество А.
2. Бинарные операции Конъюнкция(ʌ) и Дизъюнкция ( v)
3. Унарная операция отрицания (¬ или не)
4. Логические константы Истина (1) и Ложь (0)

Обобщения

Алгебраические структуры
Группа -как Группа Полугруппа  / Моноид Стеллаж и quandle Квазигруппа и петля Абелева группа Магма Группа Ли Теория групп
Кольцо -как Звенеть Rng Полукруглый Рядом с кольцом Коммутативное кольцо Интегральный домен Поле Дивизионное кольцо Теория колец
Lattice -как Решетка Полурешетка Дополненная решетка Общий заказ Алгебра Гейтинга Булева алгебра Карта решеток Теория решетки
Модуль- подобный Модуль Группа с операторами Векторное пространство Линейная алгебра
Алгебра- подобный Ассоциативный Неассоциативный Составная алгебра Алгебра Ли Оценено Биалгебра

Удаление требования существования единицы из аксиом булевой алгебры дает «обобщенные булевы алгебры». Формально дистрибутивная решетка B является обобщенной булевой решеткой, если она имеет наименьший элемент 0 и для любых элементов a и b в B, таких что a ≤ b , существует элемент x такой, что a ∧ x = 0 и a ∨ x = б. Определяя a ∖ b как единственный x такой, что (a ∧ b) ∨ x = a и (a ∧ b) ∧ x = 0, мы говорим, что структура (B, ∧, ∨, ∖, 0) является обобщенной булевой алгебры , а (B, ∨, 0) — обобщенная булева полурешетка . Обобщенные булевы решетки — это в точности идеалы булевых решеток.

Структура, удовлетворяющая всем аксиомам булевых алгебр, кроме двух аксиом дистрибутивности, называется решеткой с ортодополнениями . Ортодополняемые решетки естественным образом возникают в квантовой логике как решетки замкнутых подпространств для сепарабельных гильбертовых пространств .

Другие законы булевой алгебры

Алгебра суждений развивается, и многие заинтересовавшиеся ученые сформулировали новые законы. Наиболее известными считаются постулаты шотландского математика О. де Моргана. Он заметил и дал определение таким свойствам, как тесное отрицание, дополнение и двойное отрицание.

Тесное отрицание предполагает, что перед скобкой нет ни одного отрицания: не (А или Б)= не А или НЕ Б.

Когда операнд отрицается, независимо от своего значения, говорят о дополнении:

И, наконец, двойное отрицание само себя компенсирует. Т.е. перед операндом либо исчезает отрицание, либо остается только одно.

Свойства булевых алгебр

Рассмотрим некоторые важные свойства булевых алгебр, вытекающие из определения.

Свойство 3.5 (единственность дополнения). В булевой алгебре для любого его дополнение единственное.

Пусть для элемента найдется еще одно такое , что и .

Имеем . Воспользовавшись свойством (3.29), получим . В силу дистрибутивности и с учетом свойств элемента имеем

С учетом свойств дополнения преобразуем последнее выражение следующим образом:

Поскольку , то . Таким образом, элемент совпадает с дополнением .

Свойство 3.6 («симметричность» операции дополнения). В булевой алгебре выполняется тождество

Так как является дополнением к , то и . В то же время и . В силу единственности дополнения к элементу имеем .

Свойство 3.7. В булевой алгебре верны следующие тождества:

(3.31)

В силу свойств 3.5 и 3.6 для доказательства первого закона достаточно показать, что

и .

Преобразуя выражения в левых частях, получаем

Первое тождество доказано. Второе тождество следует из принципа двойственности.

Тождества (3.31) называют законами де Моргана для булевых алгебр.

Единственность дополнения означает, что в булевой алгебре возникает унарная операция — переход от элемента к его дополнению. Эту операцию можно ввести в сигнатуру алгебры, т.е. рассматривать булеву алгебру как алгебру вида

с двумя бинарными, одной унарной и двумя нульарными операциями, такую, что:

1) — симметричное полукольцо;2) и (для любого ).

Дополнение в булевой алгебре называют булевым дополнением, а все операции булевой алгебры — булевыми операциями.

Булевы функции от двух аргументов

Определение 9.2. Булевой функцией от двух аргументов называется функция , заданная на множестве и принимающая значения в двухэлементном множестве . Другими словами, булева функция от двух аргументов сопоставляет любой упорядоченной паре, составленной из элементов 0 и 1 (а таких упорядоченных пар будет четыре), либо 0, либо 1.

Перечислим все возможные булевы функции от двух аргументов в форме следующей таблицы:

Заметим: функции пронумерованы так, что номер функции, записанный в двоичной системе счисления, дает последовательность значений соответствующей функции. Например, двоичная запись числа 13 имеет вид: 1101. Соответствующая функция принимает следующие значения:

Многие из перечисленных функций имеют названия и специальные обозначения. Приведем их, сгруппировав функции в пары по тому принципу, что каждая функция из пары является отрицанием другой функции этой пары.

Первые две функции, которые рассматриваются, и — тождественный ноль и тождественная единица.

Далее, функция называется конъюнкцией и обозначается (или ). Таким образом, . Конъюнкция принимает значение 1 в том и только в том случае, когда оба ее аргумента принимают значение 1. Отрицание конъюнкции, функция , называется штрихом Шеффера и обозначается . Таким образом, . Эта функция принимает значение 0 в том и только в том случае, когда функция принимает значение 1, т.е. в случае, когда оба ее аргумента принимают значение 1.

Функция называется дизъюнкцией и обозначается . Таким образом, . Функция , являющаяся отрицанием функции , носит название стрелка Пирса (или функция Вебба) и обозначается . Итак, .

Функция называется импликацией и обозначается , т.е . Аргумент в этой функции называется посылкой импликации, а аргумент — ее следствием. Отрицанием импликации является функция . Специального названия она не имеет.

Функция называется антиимпликацией или обратной импликацией, потому что представляет собой импликацию с посылкой и следствием . Таким образом, . Ее отрицанием является функция , не имеющая названия.

Функция называется эквивалентностью и обозначается , так что . Она принимает значение 1 тогда и только тогда, когда оба ее аргумента принимают одинаковые значения. Функция , являющаяся отрицанием функции , называется сложением по модулю два, или суммой Жегалкина, и обозначается .

Наконец остаются еще две пары функций. В первую пару входят функции и . Первая из них принимает всегда те же самые значения, что и ее первый аргумент, т.е. , а вторая функция является отрицанием первой: . Во вторую пару входят функции и . Первая из них принимает всегда те же самые значения, что и ее второй аргумент, т.е. , а вторая функция является отрицанием первой: .

Теперь установим некоторые важнейшие свойства введенных функций. Две булевы функции и называются равными, если каждому набору значений аргументов обе функции сопоставляют один и тот же элемент из множества , т.е. для любых . Например, .

Из введенных простейших булевых функций можно строить с помощью суперпозиций более сложные булевы функции. Например, если в функцию вставить вместо аргумента функцию , то получим следующую сложную функцию: . Если в нее в свою очередь вставить вместо аргумента функцию , то получим сложную функцию . И так далее. В результате получаются булевы функции от трех, четырех и большего числа аргументов.

В следующих теоремах устанавливаются некоторые равенства одних булевых функций другим, выражающие свойства основных булевых функций.

Нормальные формы булевых функций

На основе теоремы 10.5 всякая булева функция может быть представлена некоторой формулой алгебры высказываний. Нетрудно понять, что всякая формула алгебры высказываний, равносильная формуле, представляющей некоторую булеву функцию ; будет представлять функцию, равную . В частности, одной из таких представляющих формул будет совершенная дизъюнктивная нормальная форма (если данная булева функция не равна тождественно 0, т.е. представляющая формула не тождественно ложна) или совершенная конъюнктивная нормальная форма (если данная булева функция не равна тождественно 1, т.е. представляющая формула не является тавтологией). Отыскав совершенную нормальную форму для формулы алгебры высказываний, представляющей данную булеву функцию (применяя правила, полученные в теоремах 5.2 и 5.4), можно перейти от этой формы к формульному выражению для данной булевой функции. Его будем называть совершенной (дизъюнктивной или конъюнктивной) нормальной формой булевой функции, сокращенно СДН-формой или соответственно СКН-формой. Каждая из них для данной булевой функции, если она существует, единственна.

Приобретя опыт работы с булевыми функциями, можно отыскивать их нормальные формы, не переходя к символике алгебры высказываний. При этом, если функция задана каким-то формульным выражением, то для его тождественного преобразования следует пользоваться свойствами булевых функций, установленными в теоремах 9.3–9.5, а если функция задана своими значениями на всех наборах значений аргументов (т.е. если она задана таблично), то следует применять правила, полученные в теоремах 5.2 и 5.4, переведя их предварительно на язык булевых функций.

(помощь с решением задач, обсуждение вопросов по математике).

Дистрибутивные операции.

Дистрибутивной называют пару операций, для которых
работает схема раскрытия скобок, характерная для
сложения и умножения в арифметике:

x * (y + z) = (x * y) + (x * z) и
(x + y) * z = (x * z) + (y * z),
где * и + — некоторые
логические операции.

Первую схему будем называть левой дистрибутивностью, вторую
схему — правой дистрибутивностью, а если срабатывают обе
схемы, то будем говорить о полной дистрибутивности или просто
дистрибутивности.

Здесь приведена программа на языке C, позволяющая проверить
дистрибутивность для всех возможных комбинаций бинарных
логических операций путем перебора вариантов. Она автоматически
пропускает тривиальные операции и составляет правила
дистрибутивности.

Результаты программы выглядят так.

Из полученных правил наибольший практический интерес
представляют:

x & (y z) = (x & y) (x & z)(x y) & z = (x & z) (y & z)x (y & z) = (x y) & (x z)(x & y) z = (x z) & (y z)x & (y z) = (x & y) (x & z)(x y) & z = (x & z) (y & z)

Как видите, дистрибутивность между логическим умножением
и сложением в алгебре логики такая же как в обычной
алгебре (где она называется «распределительным законом»).
Обратите внимание, что и для операций «» и «&» можно
раскрывать скобки таким же способом. Причем обе операции
оказываются равноправны: можно раскрывать скобки когда
в них стоит «&», а вне скобок — «», а можно и в обратной
ситуации — когда внутри скобок стоит «»

3.11. Что такое переключательная схема

В компьютерах и других автоматических устройствах широко применяются
электрические схемы, содержащие сотни и тысячи переключательных элементов: реле,
выключателей и т.п. Разработка таких схем весьма трудоёмкое дело. Оказалось, что
здесь с успехом может быть использован аппарат алгебры логики.

Переключательная схема — это схематическое изображение некоторого устройства, состоящего из переключателей и соединяющих их проводников, а также из входов и выходов, на которые подаётся и с которых снимается электрический сигнал.

Каждый переключатель имеет только два состояния: замкнутое и
разомкнутое. Переключателю Х поставим в соответствие логическую
переменную х, которая принимает значение 1 в том и только в том случае,
когда переключатель Х замкнут и схема проводит ток; если же переключатель
разомкнут, то х равен нулю.

Будем считать, что два переключателя Х и связаны
таким образом, что когда Х замкнут, то
разомкнут, и наоборот. Следовательно, если переключателю Х поставлена в
соответствие логическая переменная х, то переключателю должна
соответствовать переменная .

Всей переключательной схеме также можно поставить в соответствие логическую
переменную, равную единице, если схема проводит ток, и равную нулю — если не
проводит. Эта переменная является функцией от переменных, соответствующих всем
переключателям схемы, и называется функцией проводимости.

Найдем функции проводимости F некоторых переключательных схем:

a)  

Схема не содержит переключателей и проводит ток всегда, следовательно
F=1; 

б)  

Схема содержит один постоянно разомкнутый контакт, следовательно
F=0; 

в)  

Схема проводит ток, когда переключатель х замкнут, и не проводит, когда х
разомкнут, следовательно, F(x) = x; 

г)  

Схема проводит ток, когда переключатель х разомкнут, и не проводит, когда
х замкнут, следовательно, F(x) = ; 

д)  

Схема проводит ток, когда оба переключателя замкнуты, следовательно,
F(x) = x . y; 

е)  

Схема проводит ток, когда хотя бы один из переключателей замкнут,
следовательно, F(x)=x v y; 

ж)  

Схема состоит из двух параллельных ветвей и описывается функцией . 

Две схемы называются равносильными, если через одну из них проходит ток тогда и только тогда, когда он проходит через другую (при одном и том же входном сигнале). Из двух равносильных схем более простой считается та схема, функция проводимости которой содержит меньшее число логических операций или переключателей.

Задача нахождения среди равносильных схем наиболее простых является очень
важной. Большой вклад в ее решение внесли российские учёные Ю.И

Журавлев,
С.В. Яблонский и др.

При рассмотрении переключательных схем возникают две основные задачи:
синтез и анализ схемы.

СИНТЕЗ СХЕМЫ по заданным условиям ее работы сводится к следующим трём
этапам:

1. составлению функции проводимости по таблице истинности, отражающей эти
   условия;
2. упрощению этой функции;
3. построению соответствующей схемы.

АНАЛИЗ СХЕМЫ сводится к

1. определению значений её функции проводимости при всех возможных наборах
   входящих в эту функцию переменных.
2. получению упрощённой формулы.

Примеры.

1. Построим схему, содержащую 4 переключателя
x, y, z и t, такую, чтобы она проводила ток тогда и только тогда, когда замкнут
контакт переключателя t и какой-нибудь из остальных трёх контактов.

Решение. В этом случае можно обойтись без построения таблицы
истинности. Очевидно, что функция проводимости имеет вид F(x, y, z, t) =
t . (x v y v z), а схема выглядит так:

2. Построим схему с пятью переключателями,
которая проводит ток в том и только в том случае, когда замкнуты ровно четыре из
этих переключателей.

Схема имеет вид:

3. Найдем функцию проводимости схемы:

Решение. Имеется четыре возможных пути прохождения тока при замкнутых
переключателях a, b, c, d, e : через переключатели a, b; через переключатели a,
e, d; через переключатели c, d и через переключатели c, e, b. Функция
проводимости F(a, b, c, d, e) = a . b   v   a .
e . d   v   c . d   v   c .
e . b.

4. Упростим переключательные схемы:

а)  

Решение:   

Упрощенная схема:

б)  

.

Здесь первое логическое слагаемое является
отрицанием второго логического слагаемого , а
дизъюнкция переменной с ее инверсией равна 1.

Упрощенная схема :

в)  

Упрощенная схема:

г)  

Упрощенная схема:

д)  

(по
закону склеивания)

Упрощенная схема:

е)  

Решение:

Упрощенная схема:

Рекомендации

Процитированные работы

• Дэйви, BA; Пристли, HA (1990). Введение в решетки и порядок . Кембриджские математические учебники. Издательство Кембриджского университета.
• Кон, Пол М. (2003), Базовая алгебра: группы, кольца и поля , Springer, стр. 51, 70–81, ISBN 
• Гивант, Стивен; Халмос, Пол (2009), Введение в булевы алгебры , Тексты для студентов по математике , Springer , ISBN 978-0-387-40293-2.
• Падманабхан, Ранганатан; Рудяну, Серджиу (2008), Аксиомы для решеток и булевых алгебр , World Scientific, ISBN 978-981-283-454-6.

Общие ссылки

• Браун, Стивен; Вранешич, Звонко (2002), Основы цифровой логики с дизайном VHDL (2-е изд.), McGraw – Hill , ISBN 978-0-07-249938-4. См. Раздел 2.5.
• Кори, Рене; Ласкар, Дэниел (2000), Математическая логика: курс с упражнениями , Oxford University Press , ISBN 978-0-19-850048-3. См. Главу 2.
• Dahn, BI (1998), «Robbins Алгебра булевы: A Пересмотр сгенерированного компьютера Решения McCune о Robbins в проблеме», журнал алгебра , 208 (2): 526-532, DOI : .

• Халмос, Пол (1963), Лекции по булевым алгебрам , Ван Ностранд, ISBN 978-0-387-90094-0.
• Халмос, Пол ; Гивант, Стивен (1998), , Dolciani Mathematical Expositions, 21 , Математическая ассоциация Америки , ISBN 978-0-88385-327-6.
• .
• Мендельсон, Эллиотт (1970), , серия набросков Шаума по математике, McGraw – Hill , ISBN 978-0-07-041460-0
• Монк, Дж. Дональд; Бонне Р., ред. (1989), , Северная Голландия , ISBN 978-0-444-87291-3. В 3-х томах. (Том 1: ISBN  978-0-444-70261-6 , Том 2: ISBN  978-0-444-87152-7 , Том 3: ISBN  978-0-444-87153-4 )
• Сикорский, Роман (1966), Булевы алгебры , Ergebnisse der Mathematik и ихрер Гренцгебиете, Springer Verlag.
• Столл, Р. Р. (1963), Теория множеств и логика , WH Freeman, ISBN 978-0-486-63829-4. Перепечатано Dover Publications , 1979.