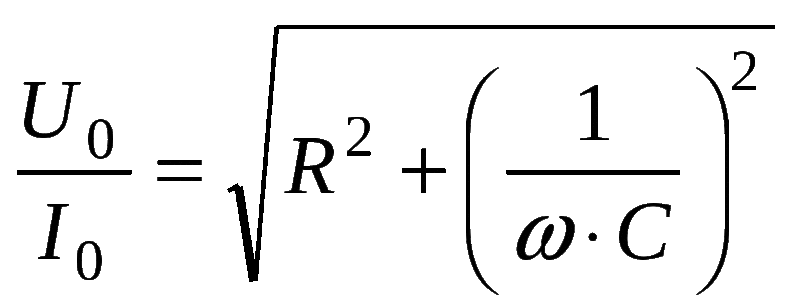Физический смысл емкостного сопротивления в цепи переменного тока

Величины и единицы измерения ёмкости и индуктивности – для новичков в радиоделе

Ёмкость конденсатора, если его представить в виде двух металлических пластин с диэлектриком между ними, зависит от площади поверхности пластин, расстояния между ними и свойств диэлектрика Есть конденсаторы переменной ёмкости, где в качестве диэлектрика выступает воздух

Рис 418 Конденсатор переменной ёмкости

Чтобы увеличить ёмкость постоянного конденсатора его обкладки изготавливают, например, из алюминиевой фольги, проложенной тонким диэлектриком Поверхность получается достаточно большой, а свёрнутая фольга занимает мало места Чем тоньше диэлектрик, тем больше ёмкость

Но при этом тонкий диэлектрик легче пробивается напряжением То есть, рабочее напряжение конденсатора становится меньше

Переменные конденсаторы небольшой ёмкости служат для подстройки, их ещё называют триммерами

Рис 419 Подстроечный конденсатор

К единице ёмкости конденсаторов применяют приставки микро, нано, пико, что означает, почти все конденсаторы имеют ёмкость меньше основной единицы, фарады Часто это можно отнести и к единицам индуктивности, где основная единица генри

Есть один вид конденсаторов, отличающийся от других, которые называют электролитическими конденсаторами Это конденсаторы большой ёмкости, но для получения такой ёмкости их заполняют электролитом Такие конденсаторы, как правило, полярные, то есть, их правильная работа зависит от правильной полярности напряжения на них Чтобы при подключении конденсатора не произошла ошибка, на корпус наносят маркировку Если электролит в процессе работы конденсатора высыхает, то конденсатор теряет ёмкость

Хотя конденсатор не пропускает постоянный электрический ток, ток утечки всё-таки есть, то есть, у сопротивления конденсатора есть активная составляющая Электролитический конденсатор, выполненный из свёрнутой ленты фольги, похож на индуктивность, что подразумевает влияние этой индуктивности на высоких частотах Чтобы избежать этого влияния, параллельно электролитическому конденсатору можно поставить керамический конденсатор

Катушки индуктивности с номиналом в десятки миллигенри выглядят как катушки:

Рис 420 Катушка индуктивности 15 мГн

А катушки индуктивности в десятки микрогенри похожи, скорее, на резисторы

Рис 221 Катушка индуктивности 10 мкГн

Такие индуктивности называют ещё дросселями и используют в фильтрах, особенно в фильтрах цепей питания высокочастотных устройств Их можно намотать на обычном резисторе с большим сопротивлением, скажем в несколько мегаом Или намотать на тонком ферритовом стержне Катушки колебательных контуров карманных радиоприёмников наматывают на ферритовый стержень, который одновременно служит магнитной антенной приёмника

Индуктивность катушки зависит от количества витков, диаметра намотки и материала, на который наматывается катушка Чтобы уменьшить влияние сопротивления провода, его стараются выбрать достаточно большого диаметра Провод высокочастотных катушек, когда количество витков небольшое, применяют посеребрённый

На высоких частотах вполне можно применять изготовление катушки в виде спирали на печатной плате Такой способ изготовления очень технологичен и имеет хорошую повторяемость параметров

Для получения больших значений индуктивности используют такие сердечники, как кольца из ферритов или сердечники из трансформаторной стали

Для точной настройки величины индуктивности катушки индуктивности часто имеют сердечники, медные или ферритовые

Раньше карманные приёмники имели довольно большое количество фильтров промежуточной частоты, выполненных с использованием катушек индуктивности

Для уменьшения влияния катушек друг на друга их помещали в защитные экраны

Каждая из катушек имела ферритовый сердечник, который позволял настроить фильтр точно на промежуточную частоту

Позже в качестве фильтров стали применять ПАВ-фильтры (фильтры на поверхностных акустических волнах) и пьезо-фильтры

Рис 222 Катушки индуктивности с подстроечными сердечниками

Tweet Нравится

Предыдущая запись: Как переводить с языка электрических схем
Следующая запись: КОНВЕРТОРЫ В УСТРОЙСТВАХ НА МИКРОСХЕМАХ

Конденсаторы как элементы схем (0)
Конденсаторы в цепи переменного тока (0)
Индуктивности (0)
БУФЕРНОЕ УСТРОЙСТВО ДЛЯ АЦП I (0)
УСТРОЙСТВО ЗАЩИТЫ ПК C ПОМОЩЬЮ ПАРОЛЯ (0)
ЛИНЕЙНЫЙ УСИЛИТЕЛЬ МОЩНОСТЬЮ 1,2 KBT И ЧАСТОТОЙ 144 МГЦ (0)
УСТРОЙСТВО ДЛЯ ВЫБОРА ФИЛЬТРОВ HA Р1Н-ДИОДЕ (0)

Способы соединения элементов

Монтаж изделия на плату может быть вертикальным или горизонтальным. При использовании нескольких изделий они могут быть соединены между собой разными способами.

Параллельное соединение

Для его организации нужно подключить группу деталей к электроцепи так, чтобы обкладки всех деталей были подсоединены напрямую к местам включения. Поскольку все компоненты получают заряд от одного источника тока, у них будет одинаковая разность потенциалов. Но так как заряд копится на каждом изделии отдельно, количество электричества на группе можно выразить как сумму количеств на ее деталях.

Это справедливо и для емкостных данных – значение для конфигурации равно сумме значений каждой единицы. Поэтому такую группу можно считать равной одному конденсатору, емкостной параметр которого равен сумме таковых для всех частей.

Последовательное соединение

Эта схема подразумевает соединение устройств одно за другим, когда к местам подключения к цепи подсоединены только два крайних изделия. Количество электричества для каждой детали будет одинаковым. При этом, чем менее емкое устройство, тем большее значение напряжения на нем будет наблюдаться.

Последовательное подключение

Смешанное соединение

Такая сложная конструкция содержит фрагменты с двумя вышеприведенными типами соединений. Чтобы подсчитать полную емкость, схему делят на простые блоки, состоящие только из деталей, соединенных каким-то одним образом. Находят эквивалентные значения для каждого блока и затем рисуют схему заново в упрощенном виде. Рассчитывают данные для получившейся системы.

Чтобы суметь подобрать подходящий конденсаторный набор, нужно уметь узнавать емкостные данные

Важно также знать, как рассчитывается показатель для конфигурации из нескольких деталей, соединенных между собой тем или иным образом

Импеданс элемента

Общее сопротивление конденсатора (импеданс) переменному сигналу складывается из трёх составляющих: ёмкостного, резистивного и индуктивного сопротивления. Все эти величины при конструировании схем, содержащих накопительный элемент, необходимо учитывать. В ином случае в электрической цепи, при соответствующей обвязке, конденсатор может вести себя как дроссель и находится в резонансе. Из всех трёх величин наиболее значимой является ёмкостное сопротивление конденсатора, но при определённых обстоятельствах индуктивное тоже оказывает влияние.

Часто при расчётах паразитные значения вроде индуктивности или активного сопротивления принимаются ничтожно малыми, а конденсатор в этом случае называется идеальным.

Полное сопротивление элемента выражается в формуле Z = (R2 + (Xl-Xc) 2 ) ½, где

Xl — индуктивность;
Xс — ёмкость;
R — активная составляющая.

Последняя возникает из-за появления электродвижущей силы (ЭДС) самоиндукции. Непостоянство тока приводит к изменению магнитного потока, поддерживающего ток ЭДС самоиндукции постоянным. Это значение определяется индуктивностью L и частотой протекающих зарядов W. Xl = wL = 2*p*f*L. Xc — ёмкостное сопротивление, зависящее от ёмкости накопителя C и частоты тока f. Xc = 1/wC = ½*p*f*C, где w — круговая частота.

Разница между ёмкостным и индуктивным значениями называется реактивным сопротивлением конденсатора: X = Xl-Xc. По формулам можно увидеть, что при увеличении частоты f сигнала начинает преобладать индуктивное значение, при уменьшении — ёмкостное. Поэтому если:

X > 0, в элементе проявляются индуктивные свойства;
X = 0, в ёмкости присутствует только активная величина;
X < 0, в элементе проявляется ёмкостное сопротивление.

Ёмкостное сопротивление

Для понимания процесса следует представить конденсатор в электрической цепи, по которой течёт переменный ток. Причём в этой цепи нет других элементов. Значение тока, проходящего через конденсатор, и напряжения, приложенного к его обкладкам, изменяется по времени. Зная любое из этих значений, можно найти другое.

Пускай ток изменяется по синусоидальной зависимости I (t) = Im * sin (w*t+ f 0). Тогда напряжение можно описать как U (t) = (Im/C*w) *sin (w*t+ f 0 -p/2). При учёте в формуле сдвига фаз на 90 градусов, возникающего между сигналами, вводится комплексная величина j, называемая мнимой единицей. Поэтому формула для нахождения тока будет выглядеть как I = U /(1/j*w*C). Но учитывая, что комплексное число только обозначает смещение напряжения относительно тока, а на их амплитудные значения не влияет, его можно убрать из формулы, тем самым значительно её упростив.

Так как по закону Ома сопротивление прямо пропорционально напряжению на участке цепи и обратно пропорционально току, то преобразуя формулы, можно будет получить следующее выражение:

Xc = 1/w*C = ½*p*f*C. Единица измерения — ом.

Становится понятно, что ёмкостное сопротивление зависит не только от ёмкости, но и от частоты. При этом чем больше эта частота, тем меньшее сопротивление конденсатор будет оказывать проходимому через него току. По отношению к ёмкости это утверждение будет обратным. Вот поэтому для постоянного тока, частота которого равна нулю, сопротивление накопителя будет бесконечно большим.

На практике всё немного по-другому. Чем ближе частота сигнала приближается к нулевому значению, тем больше становится сопротивление конденсатора, но при этом разрыв цепи наступить всё равно не может. Связанно это с током утечки. В случае когда частота стремится к бесконечности, сопротивление конденсатора должно становиться нулевым, но этого тоже не происходит — из-за присутствия паразитной индуктивности и всё того же тока утечки.

Индуктивная составляющая

При прохождении переменного сигнала через накопитель, его можно представить в виде последовательно включённой с источником питания катушки индуктивности. Эта катушка характеризуется большим сопротивлением в цепи переменного сигнала, чем постоянного. Значение силы тока в определённой точке времени находится как I = I 0 * sinw .

Приняв во внимание, что мгновенная величина напряжения U 0 обратна по знаку мгновенному значению ЭДС самоиндукции E 0, а также используя правило Ленца, можно получить выражение E = L * I, где L — индуктивность

Следовательно: U = L*w * I 0 *cosw*t = U 0 *sin (wt + p /2) , причём ток отстаёт от напряжения на p /2. Используя закон Ома и приняв, что сопротивление катушки равно w * L, получится формула для участка электрической цепи, имеющая только индуктивную составляющую: U 0 = I 0 / w * L.

Схема последовательного соединения

Когда применяется схема последовательного соединения конденсаторов, заряд каждой детали эквивалентен. С источником соединены только внешние пластины, другие – заряжаются перераспределением электрозарядов между ними. Все конденсаторы сохраняют аналогичное количество заряда на своих обкладках. Это объясняется тем, что на каждый последующий элемент поступает заряд от соседнего. Вследствие этого справедливо уравнение:

q = q1 = q2 = q3 = …

Известно, что при последовательном соединении резисторных элементов их сопротивления суммируются, но емкость конденсатора, включенного в такую электроцепь, рассчитывается по-другому.

Падение напряжения на отдельном конденсаторном элементе зависит от его емкости. Если в последовательной электроцепи имеется три конденсаторных элемента, составляется выражение для напряжения U на основании закона Кирхгофа:

U = U1 + U2 + U3,

при этом U= q/C, U1 = q/C1, U2 = q/C2, U3 = q/C3.

Подставляя значения для напряжений в обе части уравнения, получается:

q/C = q/C1 + q/C2 + q/C3.

Так как электрозаряд q – величина одинаковая, на нее можно поделить все части полученного выражения.

Результирующая формула для емкостей конденсаторов:

1/С = 1/С1 + 1/С2 + 1/С3.

Важно! Если конденсаторы подключаются в последовательную электроцепь, показатель, обратный результирующей емкости, равен совокупности обратных значений единичных емкостей. Особенности последовательного соединения

Пример. Три конденсаторных элемента подключены в последовательную цепь и обладают емкостями: С1 = 0,05 мкф, С2 = 0,2 мкФ, С3 = 0,4 мкФ. Рассчитать общую емкостную величину:

1/С = 1/0,05 + 1/0,2 + 1/0,4 = 27,5;
С = 1/27,5 = 0,036 мкФ.

Важно! Когда конденсаторные элементы включены в последовательную электроцепь, общее емкостное значение не превышает наименьшей емкости отдельного элемента. Если цепь состоит всего из двух компонентов, формула переписывается в таком виде:. Если цепь состоит всего из двух компонентов, формула переписывается в таком виде:

Если цепь состоит всего из двух компонентов, формула переписывается в таком виде:

С = (С1 х С2)/(С1 + С2).

В случае создания цепи из двух конденсаторов с идентичным емкостным значением:

С = (С х С)/(2 х С) = С/2.

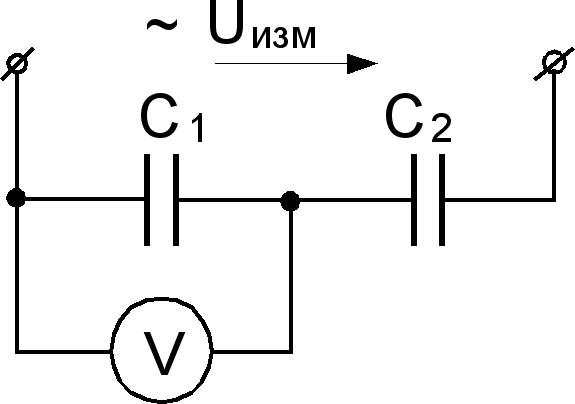
Последовательно включенные конденсаторы имеют реактивное сопротивление, зависящее от частоты протекающего тока. На каждом конденсаторе напряжение падает из-за наличия этого сопротивления, поэтому на основе такой схемы создается емкостной делитель напряжения.

Формула для емкостного делителя напряжения:

U1 = U x C/C1, U2 = U x C/C2, где:

U – напряжение питания схемы;
U1, U2 – падение напряжения на каждом элементе;
С – итоговая емкость схемы;
С1, С2 – емкостные показатели единичных элементов.

Вычисление падений напряжения на конденсаторах

К примеру, имеются сеть переменного тока 12 В и две альтернативных электроцепи подсоединения последовательных конденсаторных элементов:

первая – для подключения одного конденсатора С1 = 0,1 мкФ, другого С2 = 0,5 мкФ;
вторая – С1 = С2 = 400 нФ.

Первый вариант

Итоговая емкость электросхемы С = (С1 х С2)/(С1 + С2) = 0,1 х 0,5/(0,1 + 0,5) = 0,083 мкФ;
Падение напряжения на одном конденсаторе: U1 = U x C/C1 = 12 x 0,083/0,1 = 9,9 В
На втором конденсаторе: U2 = U x C/C2 = 12 х 0,083/0,5 = 1,992 В.

Второй вариант

Результирующая емкость С = 400 х 400/(400 + 400) = 200 нФ;
Падение напряжения U1 = U2 = 12 x 200/400 = 6 В.

Согласно расчетам, можно сделать выводы, что если подключаются конденсаторы равных емкостей, вольтаж делится поровну на обоих элементах, а когда емкостные значения различаются, то на конденсаторе с меньшей емкостной величиной напряжение увеличивается, и наоборот.

Назначение и функции конденсаторов

Конденсатор играет огромную роль как в аналоговой, так и цифровой технике. Они бывают электролитическими и керамическими, и отличаются своими свойствами, но не общей концепцией. Примеры использования:

Фильтрует высокочастотные помехи;
Уменьшает и сглаживает пульсации;
Разделяет сигнал на постоянные и переменные составляющие;
Накапливает энергию;
Может использоваться как источник опорного напряжения;
Создает резонанс с катушкой индуктивности для усиления сигнала.

Примеры использования

В усилителях обычно используются для защиты сабвуферов, фильтрации питания, термостабилизации и разделение постоянной составляющей от переменной. А электролитические в автономных схемах с микроконтроллерами могут долго обеспечивать питание за счет большой емкости.
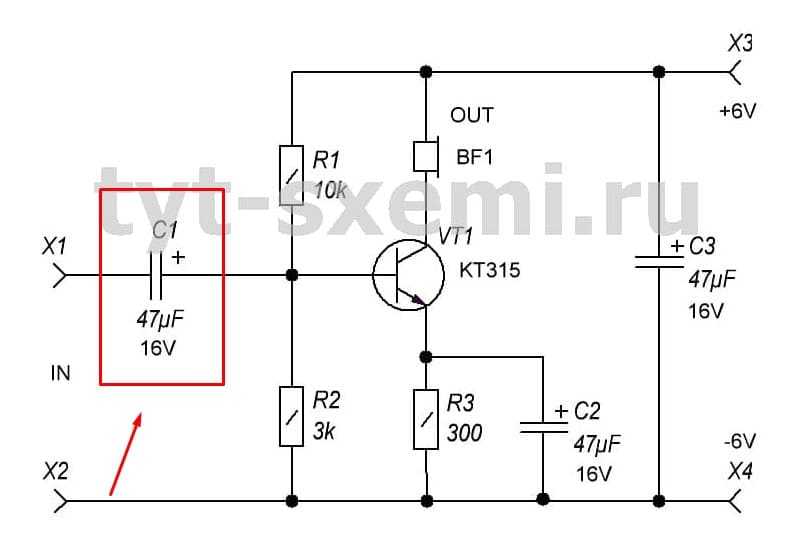
В данной схеме транзистор VT1 постоянно открыт, чтобы усиливать звук без искажений. Но если вход замнется или на него поступи постоянный ток, то транзистор откроется, перейдет в насыщение и перегреется. Чтобы этого не допустить, нужен конденсатор. С1 позволяет отделить постоянную оставляющую от переменной. Переменный сигнал легко проходит на базу транзистора, а постоянный сигнал не проходит.

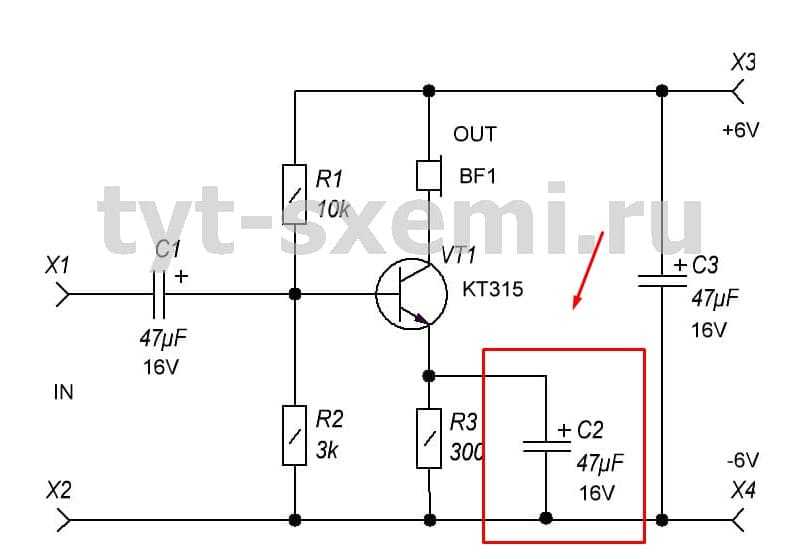
С2 совместно с резистором R3 выполняет функцию термостабилизации. Когда усилитель работает, транзистор нагревается. Это может внести искажения в сигнал. Поэтому, резистор R3 помогает удержать рабочую точку при нагреве. Но когда транзистор холодный и стабилизации не требуется резистор может уменьшить мощность усилителя. Поэтому, в дело вступает С2. Он проводит через себя усиленный сигнал шунтируя резистор, тем самым, не снижая номинальную мощность схемы. Если его емкость будет ниже расчетной, он начнет вносить фазовые искажения в выходной сигнал.

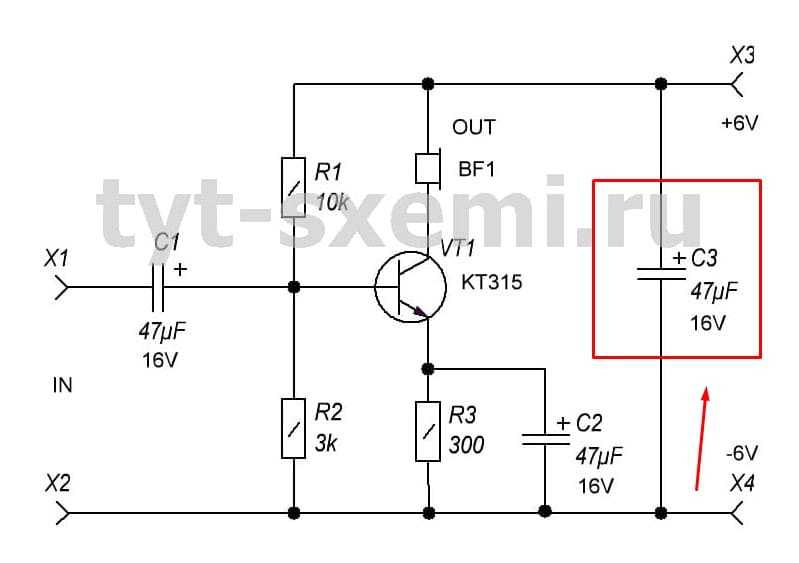
Чтобы схема качественно работала, обязательно хорошее питание. Когда схема в пиковые значения потребляет больше тока, то это всегда сильная нагрузка на источник питания. С3 фильтрует помехи по питанию и помогает снизить нагрузку. Чем больше емкость — тем лучше звук, но до определенных значений, все зависит от схемы.

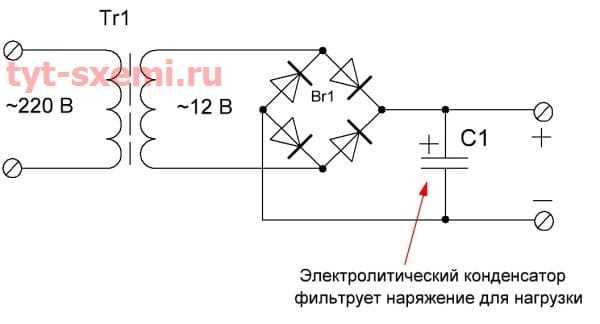
А в блоках питания используется тот же принцип, как и в предыдущей схеме по питанию, но здесь емкость нужна гораздо больше. На этой схеме емкость элеткролита может быть как 1000 мкФ, так и 10 000 мкФ.

Еще на диодный мост можно параллельно включить керамические конденсаторы, которые будут шунтировать схему от высокочастотных наводок и шума сети 220 В.

Фазовые искажения

Конденсатор может искажать переменный сигнал по фазе. Это происходит из-за неверного расчета емкости, общего сопротивления и взаимодействия с другими радиодеталями. Не стоит забывать и о том, что любая радиодеталь имеет как реактивное, так и активное сопротивление.

Post Views:
1 363

История накопителей заряда

Самое раннее письменное свидетельство получения зарядов с помощью трения принадлежит учёному Фалесу из Милета (635—543 гг. до н. э.), который описал трибоэлектрический эффект от взаимодействия янтаря и сухой шерсти. Для приблизительно 2300 последующих лет любое получение электричества заключалось в трении двух различных материалов друг о друга.

Качественный рывок в знаниях о зарядах произошёл в эпоху Просвещения — период революционного развития научной мысли в образованных кругах. В это время электричество становится популярной темой, а энтузиастами было произведено немало опытов и экспериментов с генераторами на основе трения.

Открытие явления произошло во время опытов у обоих экспериментаторов, но с той разницей, что Мюссенбрук, во-первых, сделал немало усовершенствований первоначально созданного оборудования, а во-вторых, письменно сообщил коллегам о своих достижениях. Прошло совсем немного времени и учёные мира стали создавать накопители зарядов собственных конструкций. Это были первые шаги в эволюции конденсаторов, продолжающейся и в наши дни. Основные даты хронологии появления устройств для хранения зарядов:

1746 г. — изобретение лейденской банки в результате экспериментов по доработке устройства Клейста;
1750 г. — опыты Бенджамина Франклина с батареями конденсаторов;
1837 г. — публикация Майклом Фарадеем теории диэлектрической поляризации — научной основы работы накопителей;
конец XIX в. — начало практического применения лейденских банок вместе с первыми устройствами постоянного тока;
начало XX в. — изобретение слюдяных и керамических конденсаторов.

Емкостное сопротивление в цепи переменного тока

При включении конденсатора в цепь постоянного тока, на протяжении короткого периода времени будет наблюдаться течение по цепи зарядного тока. По окончании зарядки, когда напряжение конденсатора будет соответствовать напряжению источника тока, кратковременное течение тока в цепи прекратится. Таким образом, полностью при постоянном токе будет своеобразным разрывом цепи или сопротивлением с бесконечно большим значением. При переменном токе конденсатор будет вести себя совершенно иначе. Его зарядка в такой цепи будет осуществляться поочередно в разных направлениях. Течение переменного тока в цепи в это время не прерывается.

Более подробное рассмотрение этого процесса указывает на нулевое значение напряжения в конденсаторе в момент его включения. После поступления к нему переменного напряжения сети начнется зарядка. В это время сетевое напряжение будет возрастать на протяжении первой четверти периода. По мере того как на обкладках накапливаются заряды, происходит увеличение напряжения самого конденсатора. После того как сетевое напряжение в конце первой четверти периода станет максимальным, зарядка прекращается и значение тока в цепи станет равным нулю.

Существует формула для определения тока в цепи конденсатора: I = ∆q/∆t, где q является количеством электричества, протекающим по цепи в течение промежутка времени t. В соответствии с законами электростатики, количество электричества в устройстве составит: q = C x Uc = C x U. В этой формуле С будет емкостью конденсатора, U — напряжением сети, Uc — напряжением на обкладках элемента. В окончательном виде формула тока в цепи будет выглядеть следующим образом: i = C x (∆Uc/∆t) = C x (∆U/∆t).

При наступлении второй четверти периода произойдет уменьшение сетевого напряжения и начнется разрядка конденсатора. Ток в цепи изменит свое направление и будет течь в обратную сторону. В следующей половине периода направление сетевого напряжения изменится, наступит перезарядка элемента, а потом он вновь начнет разряжаться. Ток, присутствующий в цепи с конденсаторной емкостью, будет опережать по фазе напряжение на обкладках на 90 градусов.

Установлено что изменения тока конденсатора происходят со скоростью, находящейся в пропорциональной зависимости с угловой частотой ω. Поэтому в соответствии с уже известной формулой тока в цепи i = C x (∆U/∆t), аналогично получается, что действующее значение тока также будет представлять собой пропорцию между скоростью изменения напряжения и угловой частотой ω: I = 2π x f x C x U.

Далее уже совсем несложно установить значение емкостного сопротивления или реактивного сопротивления емкости: xc = 1/2π x f x C = 1/ ω x C. Данный параметр вычисляется, когда конденсаторная емкость включается в цепь переменного тока. Поэтому в соответствии с законом Ома в цепи переменного тока с включенным конденсатором, значение силы тока будет следующим: I = U/xc, а напряжение на обкладках составит: Uc = Ic x xc.

Часть сетевого напряжения, приходящаяся на конденсатор, получила название емкостного падения напряжения. Она известна также, как реактивная слагающая напряжения, обозначаемая символом Uc. Величина емкостного сопротивления хс, так же, как и значение индуктивного сопротивления xi напрямую связана с частотой переменного тока.

ОПРЕДЕЛЕНИЕ

Конденсатор, в простейшем случае состоит из двух металлических проводников (обкладок), которые разделяет слой диэлектрика. Каждая из обкладок конденсатора имеет свой вывод и может быть подключена к электрической цепи.

Конденсатор характеризуют при помощи ряда параметров (емкость, рабочее напряжение и т. д), одной из таких характеристик является сопротивление. Конденсатор практически не пропускает постоянный электрический ток. То есть сопротивление конденсатора является бесконечно большим для постоянного тока, но это идеальный случай. Через реальный диэлектрик очень малый ток протекать может. Этот ток называют током утечки. Ток утечки является показателем качества диэлектрика, который применяется при изготовлении конденсатора. У современных конденсаторов ток утечки составляет некоторые доли микроампера. Сопротивление конденсатора в таком случае можно вычислить, используя закон Ома для участка цепи, зная величину напряжения, до которой заряжен конденсатор и ток утечки. Но обычно при решении учебных задач сопротивление конденсатора постоянному току считают бесконечно большим.

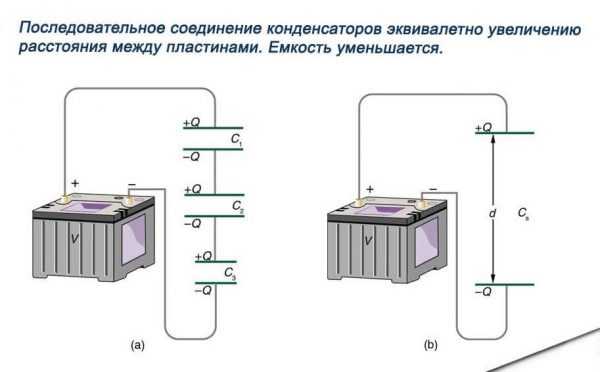
Последовательное соединение конденсаторов.

Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным (рисунок 3).

Рисунок 2. Последовательное соединение конденсаторов.

При последовательном соединении все конденсаторы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины (1 и 6), а остальные пластины (2, 3, 4 и 5) заряжаются через влияние. При этом заряд пластины 2 будет равен по величине и противоположен по знаку заряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пластины 2 и т. д.

Напряжения на различных конденсаторах будут, вообще говоря, различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения. Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.

Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.

Аналогично предыдущему случаю можно рассматривать всю группу конденсаторов, соединенных последовательно, как один эквивалентный конденсатор, между пластинами которого существует напряжение, равное сумме напряжений на всех конденсаторах группы, а заряд которого равен заряду любого из конденсаторов группы.

Возьмем самый маленький конденсатор в группе. На нем должно быть самое большое напряжение. Но напряжение на этом конденсаторе составляет только часть общего напряжения, существующего на всей группе конденсаторов. Напряжение на всей группе больше напряжения на конденсаторе, имеющем самую малую емкость. А отсюда непосредственно следует, что общая емкость группы конденсаторов, соединенных последовательно, меньше емкости самого малого конденсатора в группе.