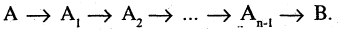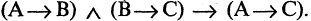Лекция 3 - логические основы работы эвм

Построение таблиц истинности для различных типов задач

Несмотря на многообразие задач, многие условия повторяются, если оставить сухие формулы, не вникая в имена, места, профессии. Разобравшись с примером один раз, можно решать аналогичные задачи без труда. Рассмотрим несколько любопытных заданий, решив при помощи логически.

Пример 2.

Известно, что если первый студент летал в Англию на стажировку, то и второй тоже летал, но неправда, что если летал третий, то и второй.

Разобьём условие на 3 простые высказывания, присвоим им буквенные обозначения:

А — «Первый студент летал в Англию»;

В — «Второй студент летал в Англию»;

С — «Третий студент летал в Англию».

Запишем выясненные данные при помощи логических операций:

Пример 3.

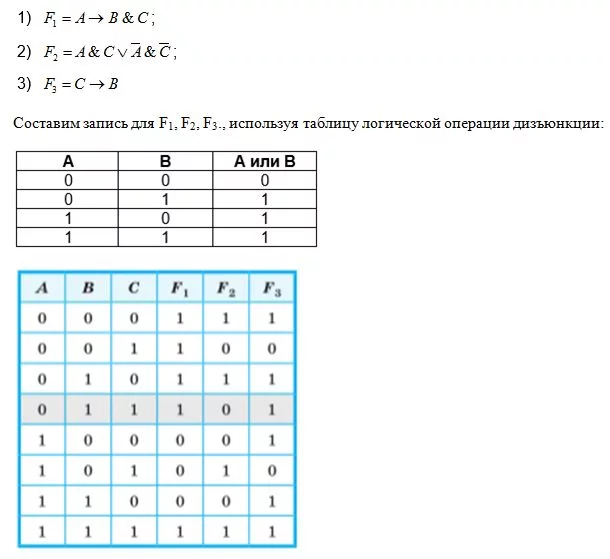
Есть три 8-ых класса (А, В, С), которые соревнуются между собой за средний бал. Учителя в начале года сделали такие предположения:

Если А получит максимальный бал, то максимальный бал получат Ви С.
А и С получат или не получат максимальный бал одновременно.
Необходимым условием получения высшего бала С класса является получение высшего бала В классом.

По завершении года оказалось, что 2 предсказания оказались верными, а одно – ошибочным.

Выясним, какие же классы добились высшего бала.

Разбиваем условие задачи на элементарные высказывания:

А – «А добьется высшего бала»;

В – «В добьется высшего бала»;

С – «С добьется высшего бала».

Запишем логические операции, описанные в примере:

Мы заполнили таблицу истинности для всех возможных значений исходных данных. В примере говорилось, что только 2 утверждения в конце года казались истинными, а 1- ложным. Такому условию отвечает 3-я строка в таблице.

Пример 4.

Во время знакомства девушка, любительница загадок, сказала, что ее имя узнать легко:

последняя – гласная (Х1);
или первая буква согласная (Х2)
вторая – согласная (Х3).

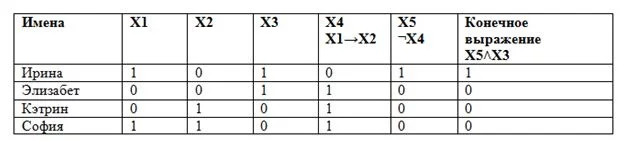
¬(Х1→Х2)VХ3

Предложенные имена: Арина, Артур, Кэтрин, София.

Решим задачу, используя таблицу.

Сначала решим пошагово, выполняя операции по приоритету:

Указанному условию соответствует первое имя.

Пример 5.

Попробуем решать задачи, в которые нет четких высказываний, истинных или ложных. В них половина информации, правда, половина – ложь, при этом неизвестно, какая именно. Под такой тип задач можно подставить любое условие, но научившись решать его, можно разобраться со всеми аналогичными.

Известно, что в олимпиаде по химии участвовали 4 ученицы 8 класса: Марина, Света, Саша и Галя. Они заняли первые 4 места. Какое место заняла каждая из девочек, если есть их высказывания о победителях, но в них лишь половина информации правдива – первая или вторая половина предложения.

Маша Марина: «Саша заняла второе место, а Света – первое».

Полина Света: «Нет, это не так, Саша – победительница, а Галя, – на втором месте».

Ольга Саша: «Зачем вы всех путаете? Третье место за Мариной, а Света – на четвертом месте».

Составляем таблица для перебора вариантов. Правду обозначаем «1», ложь – «0».

Берем любое (Марины) утверждение и принимаем его первую часть за правду. Значит, Саша – 2 место, тогда Света не 1-ое (вторая половина фразы – ложь), остальных девочек на 2 место ставим «0».

Берем утверждение второй девочки. Так как Саша не может быть победительницей, то в этой фразе первая часть – ложь, а вторая должна быть истинной. Но в нем и вторая часть – неверна (второе место за Сашей, мы так приняли в начале).Уже на второй фразе получается противоречие всему.

Итог: Победительницей олимпиады стала Светлана, на втором месте – Галина, на третьем – Марина, на последнем из четырех – Александра.

Метки

Справочник
(16)

Резонанс
(6)

TL494
(5)

Akula0083
(4)

Вечный фонарик
(4)

Радиан
(4)

Электротехническая сталь
(4)

двухчастотные генераторы
(3)

сталь
(3)

Бондаренко
(2)

Булева алгебра
(2)

Жесть
(2)

Закон
(2)

Закон Ома
(2)

Логика операций
(2)

Ом
(2)

Патент Николы Тесла
(2)

Радиант
(2)

Радиантная энегрия
(2)

Трансформатор без ОЭДС
(2)

Ферромагнетики
(2)

светодиоды
(2)

триггерные колебания
(2)

феррорезонанс
(2)

2200uf / 63v
(1)

COVID-19
(1)

ICO
(1)

IGBT
(1)

IR4426
(1)

IRF840
(1)

MC34063
(1)

Push-pull
(1)

Tesla
(1)

US 433702
(1)

US 512340
(1)

ir2153
(1)

lenta.ru
(1)

radiant energy
(1)

АПЧ
(1)

Безопасность
(1)

Биполярный транзистор
(1)

Бифилярная катушка
(1)

В. БЕЛЯКОВ
(1)

Двухтактный генератор
(1)

Демон Максвелла
(1)

Диамагнетики
(1)

Добротность
(1)

Дональд Смит
(1)

Замеры
(1)

Индуктор
(1)

КПД
(1)

КТ3102
(1)

КТ3107
(1)

Квантовая телепортация
(1)

Квантовая энергетика
(1)

Книга
(1)

Кризис
(1)

М. БАЛАШОВ
(1)

Магнетики
(1)

Максвелл
(1)

Марс
(1)

Нуль-Генератор
(1)

ОЭДС
(1)

Парамагнетики
(1)

Сергей Алексеев
(1)

Тесла
(1)

Транзистор
(1)

Трансформатор Анквича
(1)

Указ N208
(1)

Усилитель тока
(1)

Фазосдвигающая цепь
(1)

Ферриты
(1)

Электротехника
(1)

Юмор
(1)

блокинг генератор
(1)

г. Москва
(1)

детекторный приёмник
(1)

задачи
(1)

заземление
(1)

каскад с общим коллектором
(1)

контакты
(1)

криптовалюта
(1)

начало
(1)

радио
(1)

резонанс токов
(1)

самозапитка
(1)

трансмутация элементов
(1)

финансирование
(1)

цели
(1)

эмиттерный повторитель
(1)

№ 649621
(1)

Датчики параметров

Датчики параметров служат для преобразования контролируемых параметров в преобразовательных устройствах (обычно тока и напряжения) в выходное напряжение. В большинстве случаев информация о напряжении и токе требуется в виде постоянного напряжения, для чего в датчике устанавливается выпрямитель и емкостный фильтр.

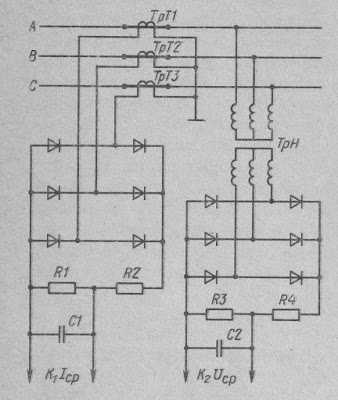
Датчики тока и напряжения (рис. 10) в трехфазной сети используют соответственно трансформаторы тока и напряжения. Трансформаторы тока устанавливаются во все три фазы и соединяются звездой (вторичные обмотки), переменное напряжение подается на выпрямитель, собранный по схеме Ларионова, а затем на делитель напряжения, состоящий из двух резисторов.

Рис. 10. Датчики параметров

На одном из устанавливается емкостный фильтр, и с него снимается напряжение пропорциональное среднему значению тока. В датчике напряжения используется трехфазный трансформатор напряжения, и выходное напряжение пропорционально среднему действующему значению переменного напряжения. К1 и К2 — коэффициенты пропорциональности.

Выходное устройство предназначено для окончательного формирования и усиления импульсов управления. В качестве ключа в схемах выходных устройств могут применяться транзисторы или тиристоры. В схемах используются элементы, позволяющие формировать импульсы специальной формы, обеспечивающие форсировку включения тиристора.

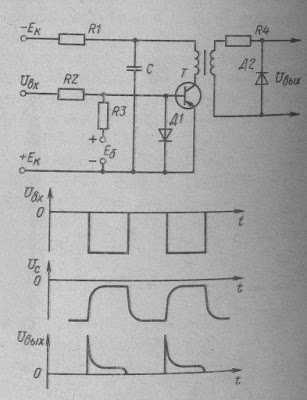
На рис. 11 показан транзисторный вариант такой схемы. Конденсатор С в промежутках между подачей входных импульсов Uвх заряжается напряжением питания Ек. При подаче входного импульса между эмиттером и базой транзистора Т, если его значение больше напряжения смещения Еб, транзистор открывается и конденсатор С разряжается на первичную обмотку трансформатора. Скорость разряда конденсатора обеспечивает уменьшение тока в первичной обмотке трансформатора и максимальное значение вторичной э.д.с. и выходного напряжения Uвых.

Рис. 11. Схема для формирования импульсов специальной формы

После разряда конденсатора ток первичной обмотки ограничивается сопротивлением резистора R1. Диод Д1 шунтирует входную цепь транзистора при подаче Uвх обратного знака. При снятии входного импульса транзистор закрывается напряжением смещения Еб.

Прямого падения напряжения на диоде Д1 от напряжения смещения достаточно доя запирания транзистора Т. Резистор R2 ограничивает базовый ток. Диод Д2 в цепи вторичной обмотки трансформатора создает разрядный контур для вторичной э. д. с. обратной полярности.

Логические схемы «И» на диодах

Схема И может быть собрана на диодах (рис. 2, б, в). Принцип построения схемы основан на том, что при наличии сигнала 0 хотя бы на одном входе сигнал 0 передается со входа на выход через открытый диод и обеспечивает запирание диодов, на входах которых действуют сигналы 1.

Рис. 2. Схема И на диодах

На рис. 2, б приведена схема для положительной логики. Сигнал 0 (е_н) по абсолютной величине больше сигнала 1 (е_в). Если на вход В подается сигнал 0, например 10 В, а на входах А и С действуют сигналы 1, например 2, то открытым окажется диод с наиболее низким потенциалом катода, т.е. диод, присоединенный ко входу В, а два других диода будут закрыты. Напряжение сигнала 0 (10 В) выделяется на резисторе Rн, с которого снимается сигнал выхода.

На рис. 2, в приведена схема И для отрицательной логики. Здесь сигнал 0 также по абсолютному значению больше сигнала 1, однако сигналы — положительные, поэтому полярность напряжения сигналов на входах изменена. При наличии сигнала 0 на входе В и сигналов 1 на остальных входах открыт диод, присоединенный ко входу В. Два других диода закрыты высоким положительным потенциалом на катодах. На выходе возникает сигнал — 0. При наличии сигналов 1 на всех входах все диоды открыты и на выходе — сигнал 1.

Основные методы доказательств

При построении любой теории выделяется некоторый набор высказываний, так называемых аксиом, истинность которых постулируется. Из аксиом чисто логическим путем может был установлена истинность некоторых других высказываний называемых теоремами. Последовательность высказываний рассматриваемой теории, каждое из которых либо является аксиомой, либо выводится из одного или более предыдущих высказываний этой последовательности по логическим правилам вывода, называется доказательством. Высказывание, которое можно доказать, называется теоремой.

Формально каждая теорема может быть выражена в форме импликации

тавтологией

Метод цепочек импликаций

Метод цепочек импликаций состоит в том, что из посылки А страивается цепочка из

В основе этого метода лежит закон цепного высказывания или закон силлогизма

Метод от противного

Метод от противного. Используя этот метод, вместо доказательства прямого следствия «из А следует В» доказывают, что из «не В» следует «не А». Этот метод основан на законе контрапозиций, имеющем следующий вид:

Метод необходимого и достаточного

Метод необходимого и достаточного. Теорема формулируется так: «Чтобы имело место А, необходимо и достаточно выполнение В». Доказательство такого вида теоремы распадается на две части:

а) доказывается, что если имеет место А, то справедливо В (В необходимо для А);

б) если имеет место В, то имеет место и А (В достаточно для А).

Доказательство таким методом базируется на законе тавтологии:

3.2. Какая связь между алгеброй логики и двоичным кодированием

Математический аппарат алгебры логики очень удобен для описания того, как
функционируют аппаратные средства компьютера, поскольку основной системой
счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а
значений логических переменных тоже два: “1” и “0”.

Из этого следует два вывода:

одни и те же устройства компьютера могут применяться для обработки и
хранения как числовой информации, представленной в двоичной системе счисления,
так и логических переменных;
на этапе конструирования аппаратных средств алгебра логики позволяет
значительно упростить логические функции, описывающие функционирование схем
компьютера, и, следовательно, уменьшить число элементарных логических
элементов, из десятков тысяч которых состоят основные узлы компьютера.

Что такое триггер?

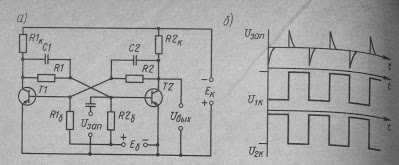
Триггер как логический элемент может осуществлять функцию памяти, так как переходит из одного устойчивого состояния в другое при наличии запускающего или переключающего сигнала. Схема симметричного триггера с внешним смещением приведена на рис. 7, а.

Триггер представляет собой двухкаскадный усилитель, где выход одного каскада связан со входом другого делителем напряжения на резисторах R — Rб. Обычно схема выполняется симметричной, т. е. соответствующие резисторы плеч (каскадов), конденсаторы и транзисторы имеют одинаковые параметры.

Рис. 7. Симметрический триггер с внешним смещением

В схеме используется источник внешнего положительного смещения Еб, и база каждого транзистора имеет потенциал, значение которого лежит между +Е_б и отрицательным потенциалом коллектора другого транзистора.

Предположим, что транзистор Т1 закрыт и напряжение на переходе эмиттер — коллектор U1к ≈ Ек (см. кривые напряжений, рис. 7, б).

При определенном подборе резисторов делителя R1 — R_2б потенциал базы транзистора Т2 будет отрицательным для насыщения.

Открытое состояние транзистора Т2 увеличивает положительный потенциал на базе транзистора Т1 и поддерживает его закрытое состояние. Чтобы вывести схему из устойчивого состояния, необходимо подать на базу закрытого транзистора отрицательный запускающий импульс или на базу открытого — положительный.

Если под действием отрицательного импульса начнет открываться транзистор Т2 (начало координат), то возникнет ток в цепи коллектора и потенциал коллектора станет выше. Благодаря делителю R2 — R_1б это же состояние будет на базе транзистора Т1, ток в цепи коллектора которого уменьшится, и потенциалы коллектора Т1 и базы Т2 станут ниже, что приведет к дальнейшему открыванию транзистора Т2. Процесс переключения триггера протекает лавинообразно, поэтому можно считать, что кривые коллекторных напряжений имеют прямоугольную форму.

Конденсаторы С1 — С2 называются ускоряющими и служат для форсирования процесса переключения триггера. В период паузы между переключениями триггера конденсатор, присоединенный к коллектору закрытого транзистора, заряжается базовым током открытого, в это же время второй конденсатор разряжается.

При лавинообразном переключении триггера базовый ток открывающегося транзистора проходит через разряженный конденсатор и не ограничивается резисторами R1 — R2.

Схема несимметричного триггера представлена в статье «Судовая пожарная сигнализация» — схема автоматического извещателя.

Простой логический пробник

Схема логического пробника для отыскания неисправностей цифровых схем, описание его возможностей и приемов работы с пробником.

Общеизвестно, что для ремонта и налаживания электронных цифровых схем необходим осциллограф. Конечно, сейчас прошли те времена, когда приходилось на заводах ремонтировать большие ЭВМ.

Зато появились устройства различного назначения на микроконтроллерах, специализированных микросхемах, большое количество устройств с использованием цифровых микросхем малой степени интеграции (еще не все предприятия и организации успели приобрести современное импортное оборудование).

Обычным авометром невозможно увидеть процессы, происходящие в импульсных схемах и сделать выводы о работе схемы в целом. Но осциллограф под рукой может оказаться не всегда. Вот в этом случае может оказать неоценимую помощь описываемый логический пробник.

Подобных устройств в литературе было описано немало и все они при одинаковом назначении все-таки имеют совершенно разные параметры: есть такие, что просто неудобны и непонятны в работе. Такие пробники выпускались отечественной промышленностью до конца прошлого века.

Много лет мне довелось пользоваться логическим пробником, конструкция которого описана ниже. Схема показала себя надежной и удобной в работе.

Основное отличие данной схемы от подобных – минимальное количество деталей при достаточно широких возможностях. Одной из особенностей схемы является наличие второго входа, что иногда позволяет обходиться без двулучевого осциллографа.

Электрическая принципиальная схема логического пробника
Описание принципиальной схемы.
Питание пробника (+5В) осуществляется от проверяемой схемы.

Исследуемый сигнал поступает на базы входных транзисторов VT1, VT2, предназначенных для увеличения входного сопротивления прибора. Далее, через диоды VD1, VD2 сигнал проходит на логические элементы D1.2, D1.3, D1.4, которые зажигают красный и зеленый светодиоды.

Приемы работы с пробником.

Свечение красного светодиода говорит о наличии на входе 1 логической единицы, а зеленого – логического нуля.

Для описываемого пробника напряжение логического нуля 0…0,4В, а логической единицы 2,4…5,0В. Если вход 1 пробника никуда не подключен, оба светодиода погашены.

Кроме показа логических уровней нуля и единицы пробник также может показывать наличие импульсов. Для этих целей служит двоичный счетчик D2, к выходам которого подсоединены светодиоды HL1…HL4 желтого цвета.

С приходом каждого импульса состояние счетчика увеличивается на единицу. Если частота следования импульсов невелика, то можно увидеть мигание светодиодов счетчика, даже если импульс длительностью несколько микросекунд появляется раз в секунду или еще реже. Такой процесс можно зафиксировать только с помощью запоминающего осциллографа – прибора достаточно дорогого и редкого.

Когда импульсы следуют с высокой частотой, кажется, что светодиоды HL1…HL4 светятся непрерывно, хотя на самом деле зажигаются импульсами.

Соотношение импульса и паузы может быть таким, что заметно свечение только лишь одного светодиода. Но если при этом счетчик продолжает считать, то значит идут импульсы. Для сброса счетчика используется кнопка S1: если после ее нажатия и отпускания светодиоды HL1…HL4 погасли и своего состояния не изменяют, то импульсов нет, а пробник показывает просто логический уровень нуля или единицы.

Несколько слов о деталях.

Диоды VD1, VD2 могут быть заменены любыми импульсными маломощными диодами. Только при этом следует помнить, что VD1 должен быть кремниевым, а VD2 обязательно германиевым: именно они разделяют уровень нуля и единицы. Транзисторы могут быть с любыми буквенными индексами, либо заменены на КТ3102 и КТ3107.

Микросхемы могут быть заменены импортными аналогами: К155ЛА3 на SN7400N, а К155ИЕ5 на SN7493N.

При работе с пробником необходимо внимательно следить за тем, чтобы не подключить питание к цепям с напряжением более 5В, а также не касаться таких цепей измерительным щупом. Подобные касания приводят к ремонту прибора.

Борис Аладышкин

3.7. Что такое сумматор

Сумматор — это электронная логическая схема, выполняющая
суммирование двоичных чисел.

Сумматор служит, прежде всего, центральным узлом арифметико-логического
устройства компьютера, однако он находит применение также и в других устройствах
машины.

Многоразрядный двоичный сумматор, предназначенный для сложения
многоразрядных двоичных чисел, представляет собой комбинацию одноразрядных
сумматоров, с рассмотрения которых мы и начнём. Условное обозначение
одноразрядного сумматора на рис. 3.8.

Рис. 3.8.

При сложении чисел A и B в одном i-ом разряде приходится иметь дело с
тремя цифрами:

1. цифра a_i первого
слагаемого;

2. цифра b_i второго
слагаемого;

3. перенос p_i–1 из младшего
разряда.

В результате сложения получаются две цифры:

1. цифра c_i для суммы;

2. перенос p_i из данного
разряда в старший.

Таким образом, одноразрядный двоичный сумматор есть устройство с тремя
входами и двумя выходами, работа которого может быть описана следующей
таблицей истинности:

Входы	Выходы
Первое слагаемое	Второе слагаемое	Перенос	Сумма	Перенос
1	1
1	1
1	1	1
1	1
1	1	1
1	1	1
1	1	1	1	1

Если требуется складывать двоичные слова длиной два и более бит, то можно
использовать последовательное соединение таких сумматоров, причём для двух
соседних сумматоров выход переноса одного сумматора является входом для
другого.

Например, схема вычисления суммы C = (с₃ c₂
c₁ c) двух двоичных трехразрядных чисел A =
(a₂ a₁ a) и B = (b₂ b₁
b) может иметь вид:

Табличный способ – этапы, особенности

Таблица истинности – табличное выражение результата логических операций для каждого отдельного набора значений переменных.

Такие таблицы позволяют абстрагироваться от маловажной информации, сосредоточиться только на связях между исходными данными, над происходящими процессами. Таким образом, человек может абстрагироваться от непонятной для него информации, решать неспецифические задачи

Метод таблиц

Чтобы использовать таблицы истинности, необходимо формализовать условие, то есть отойти от деталей задачи, обозначая первоначальную информацию при помощи букв и цифр 0 и 1.

Существует общий алгоритм построения таблиц:

Определить число логических значений/переменных (n) в примере.
Установить вид, число и тип операций

Важно заранее определить очередность действий, выразить это при помощи скобок.
Полученные данные позволяют рассчитать сколько нужно столбцов – это сумма числа переменных и операций.
Нарисовать таблицу, заполнить шапку, записав обозначение переменных и выбранные действия.
Определить, сколько существует наборов логических переменных (т.е. число строчек) по формуле m = 2n+ 1 (шапка).
Заполнить столбцы, вписав наборы значений логических переменных (0 или 1).
Записать результаты логических операций, указанных в шапке для каждой совокупности значений.
Сделать выводы на основании полученных результатов.

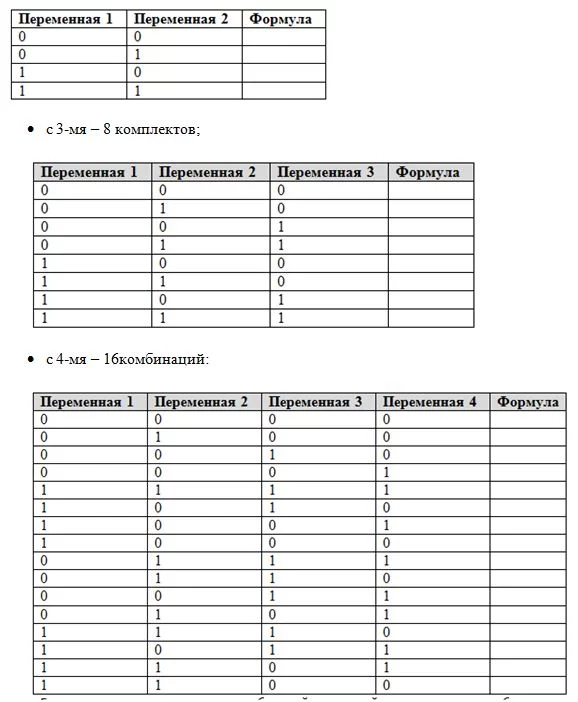
Если необходимо перебрать все значения простых выражений, то для задач:

с 2-мя переменными может быть только 4 набора логических переменных;