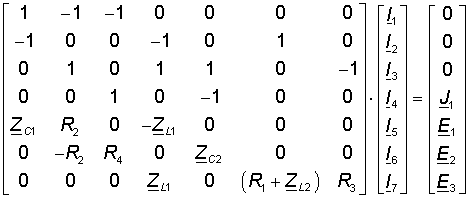Задачи на правило кирхгофа с решением

История

Пополнил ряды немецких ученых Кирхгоф в девятнадцатом столетии, когда в стране, находившаяся на пороге революции индустриальной, требовались новейших технологии. Ученые занимались поиском решений, которые могли бы ускорить развитие промышленности.

Активно занимались исследованиями в области электричества, поскольку понимали, что в будущем оно будет широко использоваться. Проблема состояла на тот момент не в том, как составлять электрические цепи из возможных элементов, а в проведении математических вычислений. Тут и появились законы, сформулированные физиком. Они очень помогли.

К узлу подходят 2 провода, а отходит один. Значение тока, текущего от узла, такое же, как сумма его, протекающего по двум остальным проводникам, т.е. идущим к нему. Правило Кирхгофа объясняет, что, при ином раскладе, накапливался бы заряд, но такого не бывает. Все знают, что всякую сложную цепь легко разделить на отдельные участки.

Но, при этом непросто определить путь, по которому он проходит. Тем более, что на различных участках сопротивления не одинаковы, поэтому и распределение энергии не будет равномерным.

В соответствие со Вторым правилом Кирхгофа, энергия электронов на каждом из замкнутых участков электрической цепи равняется нулю – нулю равняется всегда в таком контуре суммарное значение напряжений. Если бы нарушилось данное правило, энергия электронов при прохождении определенных участков, уменьшалась бы или увеличивалась. Но, этого не наблюдается.

Примеры расчета цепей

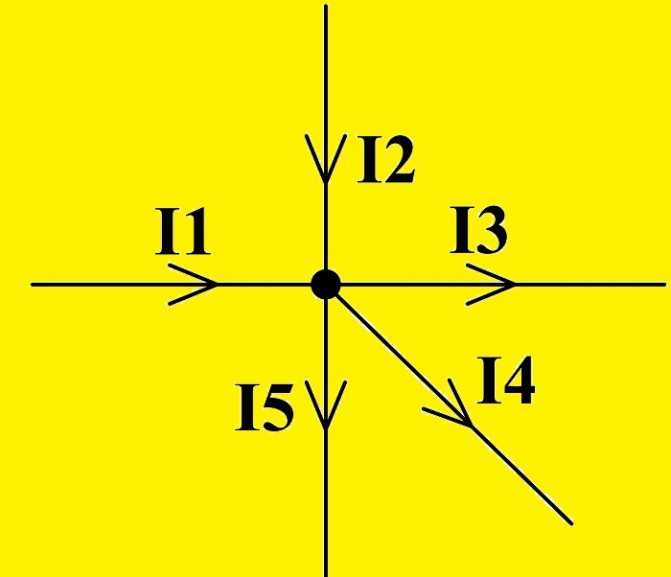
Рассмотрим ещё раз рисунок 3. На нём изображено 4 разнонаправленных вектора: i1, i2, i3, i4. Из них – два входящие ( i2, i3) и два исходящие из узла (i1, i4). Положительными будем считать те векторы, которые направлены в точку соединения ветвей, а остальные – отрицательными.

Тогда, по формуле Кирхгофа, составим уравнение и запишем его в следующем виде: – i1 + i2 + i3 – i4 = 0.

На практике такие узлы являются частью контуров, обходя которые можно составить ещё несколько линейных уравнений с этими же неизвестными. Количество уравнений всегда достаточно для решения задачи.

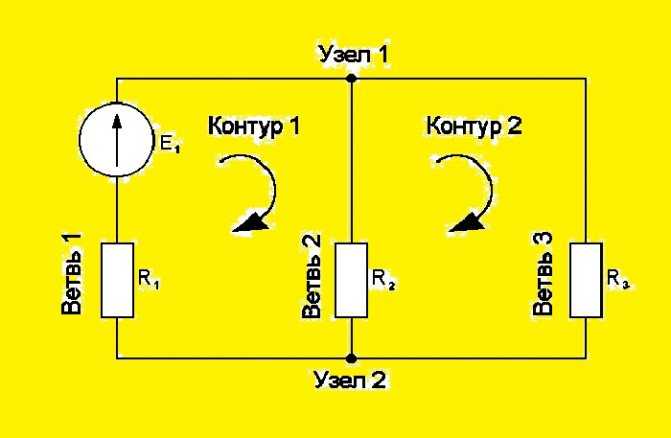
Рассмотрим алгоритм решения на примере рис. 5.

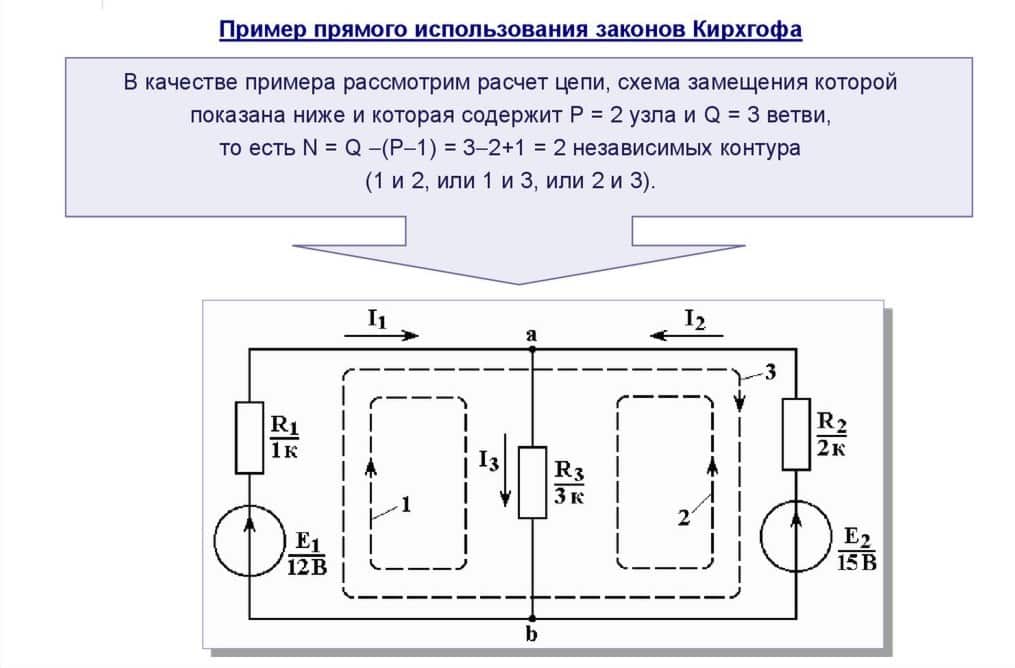
Рис. 5. Пример для расчёта

Схема содержит 3 ветви и два узла, которые образуют три пары по два независимых контура:

1. 1 и 2.
2. 1 и 3.
3. 2 и 3.

Запишем независимое уравнение, выполняющееся, например, в точке а. Из первого правила Кирхгофа вытекает: I1 + I2 – I3 = 0.

Воспользуемся вторым правилом Кирхгофа. Для составления уравнений можно выбрать любой из контуров, но нам необходимы контуры с узлом а, так как для него мы уже составили уравнение. Это будут контуры 1 и 2.

Пишем уравнения:

Решаем систему уравнений:

Так как значения R и E известны (см. рисунок 5), мы придём к системе уравнений:

Решая эту систему, получим:

1. I1 = 1,36 (значения в миллиамперах).
2. I2 = 2,19 мА.;
3. I3 = 3,55 мА.

Потенциал узла а равен: Ua = I3*R3 = 3,55 × 3 = 10,65 В. Чтобы убедиться в верности наших расчётов, проверим выполнение второго правила по отношению к контуру 3:

E1 – E2 + I1R1+ I2R2 = 12 – 15 + 1,36 – 4,38 = – 0,02 ≈ 0 (с учётом погрешностей, связанных с округлениями чисел при вычислениях).

Если проверка выполнения второго правила успешно завершена, то расчёты сделаны правильно, а полученные данные являются достоверными.

Применяя правила (законы) Кирхгофа можно вычислять параметры электрической энергии для магнитных цепей.

Источник

Пример

Предположим, электрическая сеть состоит из двух источников напряжения и трех резисторов.

Согласно первому закону:

я1-я2-я3знак равно{\ displaystyle i_ {1} -i_ {2} -i_ {3} = 0 \,}

Применение второго закона к замкнутой цепи s ₁ и замена напряжения с помощью закона Ома дает:

-р2я2+E1-р1я1знак равно{\ displaystyle -R_ {2} i_ {2} + {\ mathcal {E}} _ {1} -R_ {1} i_ {1} = 0}

Второй закон, опять же в сочетании с законом Ома, примененный к замкнутой цепи s _2, дает:

-р3я3-E2-E1+р2я2знак равно{\ displaystyle -R_ {3} i_ {3} — {\ mathcal {E}} _ {2} — {\ mathcal {E}} _ {1} + R_ {2} i_ {2} = 0}

Это приводит к системе линейных уравнений в I ₁ , I ₂ , I ₃ :

{я1-я2-я3знак равно-р2я2+E1-р1я1знак равно-р3я3-E2-E1+р2я2знак равно{\ displaystyle {\ begin {cases} i_ {1} -i_ {2} -i_ {3} & = 0 \\ — R_ {2} i_ {2} + {\ mathcal {E}} _ {1} — R_ {1} i_ {1} & = 0 \\ — R_ {3} i_ {3} — {\ mathcal {E}} _ {2} — {\ mathcal {E}} _ {1} + R_ {2 } i_ {2} & = 0 \ end {cases}}}

что эквивалентно

{я1+(-я2)+(-я3)знак равнор1я1+р2я2+я3знак равноE1я1+р2я2-р3я3знак равноE1+E2{\ displaystyle {\ begin {cases} i_ {1} + (- i_ {2}) + (- i_ {3}) & = 0 \\ R_ {1} i_ {1} + R_ {2} i_ {2 } + 0i_ {3} & = {\ mathcal {E}} _ {1} \\ 0i_ {1} + R_ {2} i_ {2} -R_ {3} i_ {3} & = {\ mathcal {E }} _ {1} + {\ mathcal {E}} _ {2} \ end {case}}}

Предполагая

р1знак равно100Ω, р2знак равно200Ω, р3знак равно300Ω{\ Displaystyle R_ {1} = 100 \ Omega, \ R_ {2} = 200 \ Omega, \ R_ {3} = 300 \ Omega}

E1знак равно3V,E2знак равно4V{\ displaystyle {\ mathcal {E}} _ {1} = 3 {\ text {V}}, {\ mathcal {E}} _ {2} = 4 {\ text {V}}}

решение

{я1знак равно11100Ая2знак равно4275Ая3знак равно-3220А{\ displaystyle {\ begin {cases} i_ {1} = {\ frac {1} {1100}} {\ text {A}} \\ i_ {2} = {\ frac {4} {275} } {\ text {A}} \\ i_ {3} = — {\ frac {3} {220}} {\ text {A}} \ end {case}}}

Ток i ₃ имеет отрицательный знак, что означает, что предполагаемое направление i ₃ было неправильным, и i ₃ фактически течет в направлении, противоположном красной стрелке, обозначенной i ₃ . Ток в R ₃ течет слева направо.

Закон Кирхгофа для магнитной цепи

Применение независимых уравнений возможно и при расчётах магнитных цепей. Сформулированные выше правила Кирхгофа справедливы и для вычисления параметров магнитных потоков и намагничивающих сил.

Рис. 4. Магнитные контуры цепей

В частности: ∑Ф=0.

То есть, для магнитных потоков первое правило Кирхгофа можно выразить словами: «Алгебраическая сумма всевозможных магнитных потоков относительно узла магнитной цепи равняется нулю.

Сформулируем второе правило для намагничивающих сил F: «В замкнутом магнитном контуре алгебраическая сумма намагничивающих сил приравнивается к сумме магнитных напряжений». Данное утверждение выражается формулой: ∑F=∑U или ∑Iω = ∑НL, где ω – количество витков, H – напряжённость магнитного поля, символ L обозначает длину средней линии магнитопровода. ( Условно принимается, что каждая точка этой линии совпадает с линиями магнитной индукции).

Второе правило, применяемое для вычисления магнитных цепей, есть не что иное, как альтернативная форма представления закона полного тока.

При совпадении векторов магнитного потока с направлениями обхода (на некоторых участках), падение напряжения на этих ветвях берём со знаком « + », а встречные ему – со знаком « – ».

Демонстрация закона напряжений Кирхгофа в параллельной цепи

Правило напряжений Кирхгофа (второй закон Кирхгофа) будет работать вообще для любой конфигурации схемы, а не только для простых последовательных цепей

Обратите внимание, как это работает для следующей параллельной схемы:. Рисунок 7 – Параллельная схема из резисторов

Рисунок 7 – Параллельная схема из резисторов

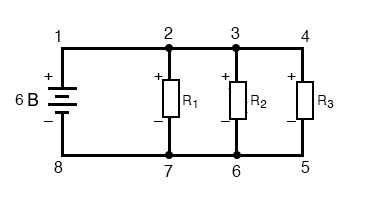
При параллельной схеме напряжение на каждом резисторе равно напряжению питания: 6 вольт. Суммируя напряжения вдоль контура 2-3-4-5-6-7-2, мы получаем:

\

Обратите внимание, что конечное (суммарное) напряжение я обозначил как E2-2. Поскольку мы начали наше пошаговое прохождение по контуру в точке 2 и закончили в точке 2, алгебраическая сумма этих напряжений будет такой же, как напряжение, измеренное между той же точкой (E2-2), которое, конечно, должно быть равно нулю

1.10. Правила Кирхгофа для разветвленных цепей

Для упрощения расчетов сложных электрических цепей, содержащих неоднородные участки, используются правила Кирхгофа, которые являются обобщением закона Ома на случай разветвленных цепей.

В разветвленных цепях можно выделить узловые точки (узлы), в которых сходятся не менее трех проводников (рис. 1.10.1). Токи, втекающие в узел, принято считать положительными; вытекающие из узла – отрицательными.

Рисунок 1.10.1. Узел электрической цепи. I1, I2 > 0; I3, I4 <� 0

В узлах цепи постоянного тока не может происходить накопление зарядов. Отсюда следует первое правило Кирхгофа:

Алгебраическая сумма сил токов для каждого узла в разветвленной цепи равна нулю:

I1 + I2 + I3 + … + In = 0.

Первое правило Кирхгофа является следствием закона сохранения электрического заряда.

В разветвленной цепи всегда можно выделить некоторое количество замкнутых путей, состоящих из однородных и неоднородных участков. Такие замкнутые пути называются контурами. На разных участках выделенного контура могут протекать различные токи. На рис. 1.10.2 представлен простой пример разветвленной цепи. Цепь содержит два узла a и d, в которых сходятся одинаковые токи; поэтому только один из узлов является независимым (a или d).

Рисунок 1.10.2. Пример разветвленной электрической цепи. Цепь содержит один независимый узел (a или d) и два независимых контура (например, abcd и adef)

В цепи можно выделить три контура abcd, adef и abcdef. Из них только два являются независимыми (например, abcd и adef), так как третий не содержит никаких новых участков.

Второе правило Кирхгофа является следствием обобщенного закона Ома.

Запишем обобщенный закон Ома для участков, составляющих один из контуров цепи, изображенной на рис. 1.10.2, например, abcd. Для этого на каждом участке нужно задать положительное направление тока и положительное направление обхода контура. При записи обобщенного закона Ома для каждого из участков необходимо соблюдать определенные «правила знаков», которые поясняются на рис. 1.10.3.

Рисунок 1.10.3. «Правила знаков»

Для участков контура abcd обобщенный закон Ома записывается в виде:

Для участка bc: I1R1 = Δφbc – 1.

Для участка da: I2R2 = Δφda – 2.

Складывая левые и правые части этих равенств и принимая во внимание, что Δφbc = – Δφda , получим:

I1R1 + I2R2 = Δφbc + Δφda – 1 + 2 = –1 – 2.

Аналогично, для контура adef можно записать:

– I2R2 + I3R3 = 2 + 3.

Второе правило Кирхгофа можно сформулировать так: алгебраическая сумма произведений сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока на этом участке равна алгебраической сумме ЭДС вдоль этого контура.

Первое и второе правила Кирхгофа, записанные для всех независимых узлов и контуров разветвленной цепи, дают в совокупности необходимое и достаточное число алгебраических уравнений для расчета значений напряжений и сил токов в электрической цепи. Для цепи, изображенной на рис. 1.10.2, система уравнений для определения трех неизвестных токов I1, I2 и I3 имеет вид:

I1R1 + I2R2 = – 1 – 2,

– I2R2 + I3R3 = 2 + 3,

– I1 + I2 + I3 = 0.

Таким образом, правила Кирхгофа сводят расчет разветвленной электрической цепи к решению системы линейных алгебраических уравнений. Это решение не вызывает принципиальных затруднений, однако, бывает весьма громоздким даже в случае достаточно простых цепей. Если в результате решения сила тока на каком-то участке оказывается отрицательной, то это означает, что ток на этом участке идет в направлении, противоположном выбранному положительному направлению.

Модель. Цепи постоянного тока

Модель. Конденсаторы в цепях постоянного тока

 

§ 15. Второй закон Кирхгофа. Применение законов Кирхгофа для расчета электрических цепей

При расчете электрических цепей часто приходится встречаться с цепями, которые образуют замкнутые контуры. В состав таких контуров, помимо сопротивлений, могут входить еще электродвижущие силы.

На рис. 35 представлена часть сложной электрической цепи в виде замкнутого контура АБВГ. На схеме указаны полярность электродвижущих сил E₁, E₂, E₃ и направления токов I₁, I₂, I₃ и I₄, протекающих на различных участках цепи.

Рис. 35. Участок сложной электрической цепи

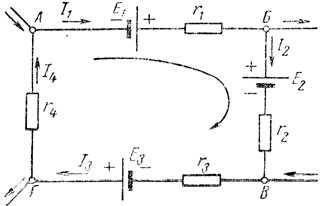
Обходим контур от точки А в произвольном направлении, например по часовой стрелке. Рассмотрим каждый из участков рассматриваемого контура. На первом участке разность потенциалов между точками А и Б, или, что то же самое, напряжение U_AБ, равна э.д.с. Е₁ минус падение напряжения I₁r₁. Аналогично будет и на других участках цепи:

на участке АБ φА - φБ = Е1 - I1r1; 
на участке БВ φБ - φВ = -Е2 - I2r2; 
на участке ВГ φВ - φГ = E3 - I3r3; 
на участке ГА φГ - φА = I4r4.

Складывая левые и правые части уравнения, получим:

φ_A — φ_Б + φ_Б — φ_В + φ_В — φ_Г + φ_Г — φ_А = E₁ — I₁r₁ — E₂ — I₂r₂ + E₃ I₃r₃ + I₄r₄;
0 = E₁ — I₁r₁ — E₂ — I₂r₂ + E₃ — I₃r₃ + I₄r₄.

Перенося произведения (I⋅r) в одну часть, а электродвижущие силы (Е) в другую часть, получим

-E₁ + E₂ — E₃ = — I₁r₁ — I₂r₂ — I₃r₃ + I₄r₄.

Или в общем виде

ΣE = ∑I ⋅ r.

Это выражение представляет собой второй закон Кирхгофа. Формула показывает, что во всяком замкнутом контуре алгебраическая сумма электродвижущих сил равна алгебраической сумме падений напряжений.

По второму закону Кирхгофа,

∑E = ∑Ir.

Для простейшей замкнутой цепи с одной э.д.с. Е (рис. 36)

E = Ir + Ir = I(r + r),

откуда

I = E/_r+r.

Рис. 36. Простой замкнутый контур

Мы получили формулу закона Ома для замкнутой цепи.

Следовательно, закон Ома является частным случаем 2-го закона Кирхгофа.

При расчете электрических цепей применяют различные методы расчета. Выбор того или иного метода зависит от конфигурации цепи, числа э.д.с., заданных величин.

Как правило, расчет неразветвленных цепей с любым числом э.д.с., а также расчет сложных цепей с одной э.д.с. легче производить, применяя закон Ома.

Расчет сложных цепей с несколькими э.д.с. производят с помощью уравнений 1-го и 2-го законов Кирхгофа.

Расчет сложной цепи методом законов Кирхгофа производят в следующем порядке:

Условно задаются направлениями токов в различных участках цепи.

Определяют число уравнений, которое необходимо составить для решения задачи. Если известны все э.д.с. и сопротивления цепи, число уравнений должно быть равно числу неизвестных токов.

Для составления уравнений вначале используют уравнения 1-го закона Кирхгофа. Число уравнений 1-го закона Кирхгофа на единицу меньше числа узловых точек в схеме. Остальное число уравнений составляют по 2-му закону Кирхгофа.

Для этого намечают контуры, направление обхода этих контуров и приступают к составлению уравнений. Если направление обхода не совпадает с направлениями э.д.с. или с направлениями токов на отдельных участках контура, то величины э.д.с. и падения напряжения I⋅r входят в уравнения со знаком минус.

Решая систему уравнений, находят величину токов,

Если окажется, что в результате решения уравнений некоторые из токов получились отрицательными, то это значит, что направление этих токов было выбрано неправильно. Надо изменить направление токов на схеме.

Проверка правильности решения производится путем подстановки полученных значений токов в одно из составленных уравнений.

Решим несколько задач, используя закон Ома и оба закона Кирхгофа.

Пример 30. Найти токи в цепи, представленной на рис. 37. Выберем произвольно положительное направление тока. Обходя контур по часовой стрелке, пишем уравнение второго закона Кирхгофа:

-E₁ + E₂ = Ir₁ + Ir₂;
-1,9 + 1,3 = I(2 + 3);
-0,6 = 5I, I = -0,12 а.

Рис. 37. Электрическая цепь (к примеру 30)

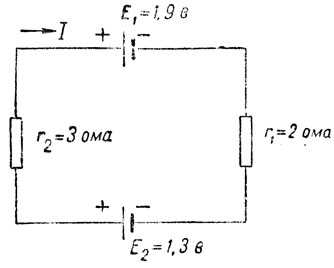
Знак минус означает, что выбранное нами направление тока противоположно его действительному направлению.

Пример 31. Дана электрическая цепь (рис. 38). Определить токи на отдельных участках.

Рис. 38. Электрическая цепь (к примеру 31)

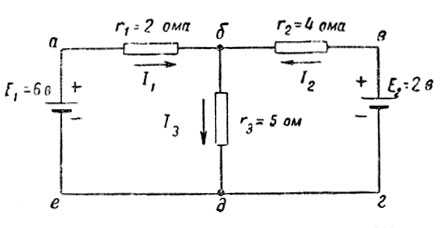
Произвольно выбираем положительные направления токов.

Для контура абде

6 = 2I₁ + 5I₃. (1)

Для контура авге

6 — 2 = 2I₁ — 4I₂. (2)

Для точки б, по первому закону Кирхгофа,

I₃ = I₁ + I₂. (3)

Имеем три уравнения с тремя неизвестными. Решая их, находим величину и направление токов. Подставляя значение тока I₃ из уравнения (3) в уравнение (1), получим

 6 = 2I1 + 5I1 + 5I2;
 6 = 7I1 + 5I2 
+
 2 = I1 - 2I2

или

 12 = 14I1 + 10I2 
+ 
 10 = 5I1 + 10I2.

Складывая два последних уравнения, имеем:

22 = 19I₁, откуда I₁ = 1,156 а,

подставляем значение I₁ в уравнение (1):

6 = 2 ⋅ 1,156 + 5I₃,

I3 =	6 — 2 ⋅ 1,156	= 0,74 а.
5

Подставляем значение I₁ в уравнение (2):

2 = 1,156 — 2I₂,

откуда

I2 =	— 2 + 1,156	= — 0,422 a.
2

Знак минус показывает, что действительное направление тока I₂ обратно принятому нами направлению.

Законы Кирхгофа для расчёта электрических цепей

При расчёте электрических цепей, в том числе для целей моделирования, широко применяются законы Кирхгофа, позволяющие полностью определить режим её работы.

Воспользуйтесь программой онлайн-расчёта электрических цепей.

Прежде чем перейти к самим законам Кирхгофа, дадим определение ветвей и узлов электрической цепи.

Ветвью электрической цепи называется такой её участок, который состоит только из последовательно включённых источников ЭДС и сопротивлений, вдоль которого протекает один и тот же ток. Узлом электрической цепи называется место (точка) соединения трёх и более ветвей. При обходе по соединённым в узлах ветвям можно получить замкнутый контур электрической цепи. Каждый контур представляет собой замкнутый путь, проходящий по нескольким ветвям, при этом каждый узел в рассматриваемом контуре встречается не более одного раза .

Первый закон Кирхгофа

Первый закон Кирхгофа применяется к узлам и формулируется следующим образом: алгебраическая сумма токов в узле равна нулю:

∑i = 0,

или в комплексной форме

∑I = 0.

Второй закон Кирхгофа

Второй закон Кирхгофа применяется к контурам электрической цепи и формулируется следующим образом: в любом замкнутом контуре алгебраическая сумма напряжений на сопротивлениях, входящих в этот контур, равна алгебраической сумме ЭДС:

∑Z ∙ I = ∑E.

Количество уравнений, составляемых для электрической цепи по первому закону Кирхгофа, равно Nу – 1, где Nу – число узлов. Количество уравнений, составляемой для электрической цепи по второму закону Кирхгофа, равно Nв – Nу + 1, где Nв – число ветвей. Количество составляемых уравнений по второму закону Кирхгофа легко определить по виду схемы: для этого достаточно посчитать число «окошек» схемы, но с одним уточнением: следует помнить, что контур с источником тока не рассматривается.

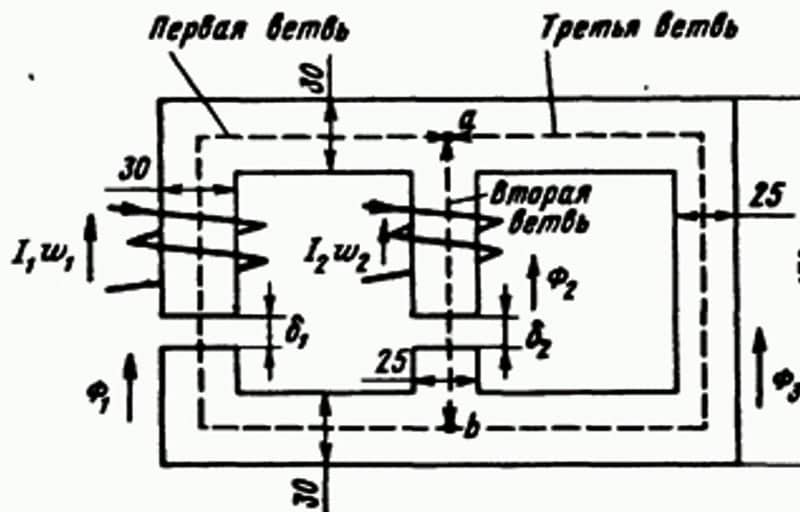
Опишем методику составления уравнений по законам Кирхгофа. Рассмотрим её на примере электрической цепи, представленной на рис. 1.

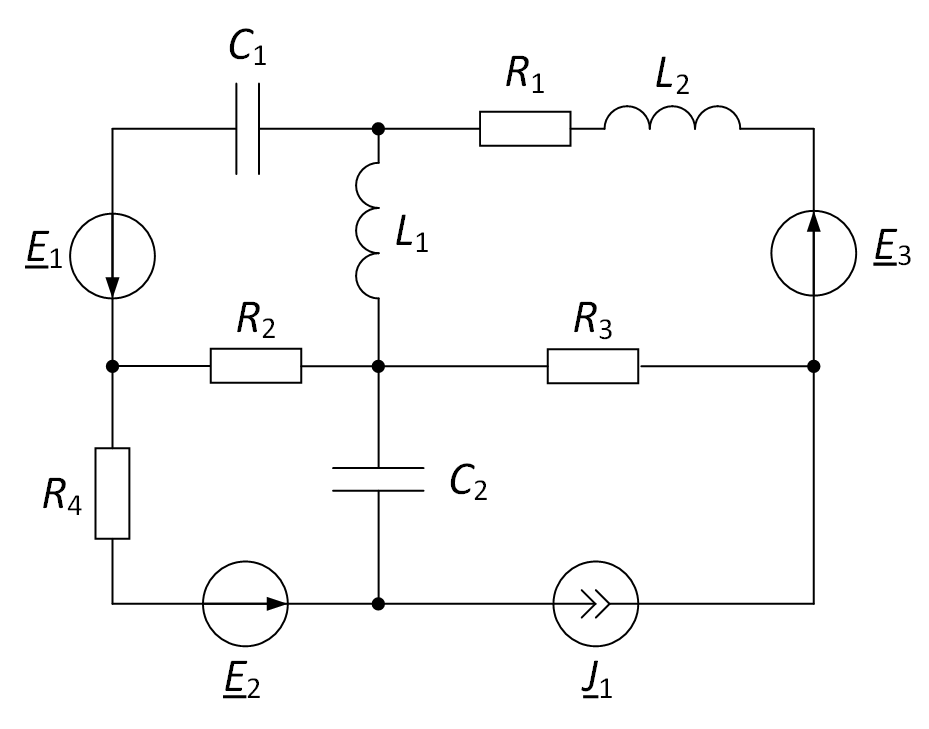
Рис. 1. Рассматриваемая электрическая цепь

Для начала необходимо задать произвольно направления токов в ветвях и задать направления обхода контуров (рис. 2).

Рис. 2. Задание направления токов и направления обхода контуров для электрической цепи

Количество уравнений, составляемых по первому закону Кирхгофа, в данном случае равно 5 – 1 = 4. Количество уравнений, составляемых по второму закону Кирхгофа, равно 3, хотя «окошек» в данном случае 4. Но напомним, что «окошко», содержащее источник тока J1, не рассматривается.

Составим уравнения по первому закону Кирхгофа. Для этого «втекающие» в узел токи будем брать со знаком «+», а «вытекающие» — со знаком «-». Отсюда для узла «1 у.» уравнение по первому закону Кирхгофа будет выглядеть следующим образом:

I1 – I2 – I3 = 0;

для узла «2 у.» уравнение по первому закону Кирхгофа будет выглядеть следующим образом:

—I1 – I4 + I6 = 0;

для узла «3 у.»:

I2 + I4 + I5 – I7 = 0;

для узла «4 у.»:

I3 – I5 – J1 = 0

Уравнение для узла «5 у.» можно не составлять.

Составим уравнения по второму закону Кирхгофа. В этих уравнениях положительные значения для токов и ЭДС выбираются в том случае, если они совпадают с направлением обхода контура. Для контура «1 к.» уравнение по второму закону Кирхгофа будет выглядеть следующим образом:

ZC1 ∙ I1 + R2 ∙ I2 – ZL1 ∙ I4 = E1;

для контура «2 к.» уравнение по второму закону Кирхгофа будет выглядеть следующим образом:

-R2 ∙ I2 + R4 ∙ I3 + ZC2 ∙ I5 = E2;

для контура «3 к.»:

ZL1 ∙ I4 + (ZL2 + R1) ∙ I6 + R3 ∙ I7 = E3,

где ZC = — 1/(ωC), ZL = ωL.

Таким образом, для того, чтобы найти искомые токи, необходимо решить следующую систему уравнений:

В данном случае это система из 7 уравнений с 7 неизвестными. Для решения данной системы уравнений удобно пользоваться Matlab. Для этого представим эту систему уравнений в матричной форме:

Для решения данной системы уравнений воспользуемся следующим скриптом Matlab:

>> syms R1 R2 R3 R4 Zc1 Zc2 Zl1 Zl2 J1 E1 E2 E3; >> A = ; >> b = ; >> I = A\b

В результате получим вектор-столбец I токов из семи элементов, состоящий из искомых токов, записанный в общем виде. Видим, что программный комплекс Matlab позволяет существенно упростить решение сложных систем уравнений, составленных по законам Кирхгофа.

Список использованной литературы

1. Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия», 1975.

Рекомендуемые записи

• Метод контурных токов для расчёта электрических цепей При расчёте электрических цепей, помимо законов Кирхгофа, часто применяют метод контурных токов. Метод контурных токов…
• Метод фазных координат: пример расчёта матрицы передачи Расчёт матриц передачи многополюсников различной формы осуществляется достаточно просто. Матрицы передачи — это математическое описание рассматриваемой…

Ограничения

Законы Кирхгофа для схемы являются результатом модели с сосредоточенными элементами, и оба зависят от модели, применимой к рассматриваемой схеме. Когда модель неприменима, законы не применяются.

Текущий закон зависит от предположения, что чистый заряд в любом проводе, соединении или сосредоточенном компоненте постоянен. Когда электрическое поле между частями схемы не является незначительным, например, когда два провода имеют емкостную связь , это может быть не так. Это происходит в высокочастотных цепях переменного тока, где модель с сосредоточенными элементами больше не применима. Например, в линии передачи плотность заряда в проводнике будет постоянно колебаться.

В линии передачи чистый заряд в разных частях проводника изменяется со временем. В прямом физическом смысле это нарушает KCL.

С другой стороны, закон напряжения основан на том факте, что действие изменяющихся во времени магнитных полей ограничено отдельными компонентами, такими как индукторы. В действительности индуцированное электрическое поле, создаваемое индуктором, не ограничено, но поля утечки часто незначительны.

Моделирование реальных схем с сосредоточенными элементами

Приближение сосредоточенных элементов для схемы является точным на низких частотах. На более высоких частотах утечки потоков и различные плотности заряда в проводниках становятся значительными. До некоторой степени все еще возможно моделировать такие схемы, используя паразитные компоненты . Если частоты слишком высоки, может быть более целесообразным моделировать поля напрямую, используя моделирование методом конечных элементов или другие методы .

Чтобы смоделировать схемы, чтобы можно было использовать оба закона, важно понимать разницу между физическими элементами схемы и идеальными элементами с сосредоточенными параметрами. Например, провод — не идеальный проводник

В отличие от идеального проводника, провода могут индуктивно и емкостно соединяться друг с другом (и с самими собой) и иметь конечную задержку распространения. Реальные проводники можно моделировать в терминах сосредоточенных элементов, учитывая паразитные емкости, распределенные между проводниками, для моделирования емкостной связи или паразитные (взаимные) индуктивности для моделирования индуктивной связи. Провода также имеют некоторую самоиндукцию, поэтому необходимы разделительные конденсаторы .

Правила (законы) Кирхгофа простыми словами

На практике часто встречаются задачи по расчётам параметров токов и напряжений в различных разветвлённых цепях. В качестве инструмента для расчётов используют правила Кирхгофа (в некоторой литературе их называют еще законами, хотя это не совсем корректно) – одни из фундаментальных правил, которые совместно с законами Ома позволяет определять параметры независимых контуров в самых сложных цепях.

Учёный Густав Киргхоф сформулировал два правила , для понимания которых введено понятие узла, ветви, контура. В нашей ситуации ветвью будем называть участок, по которому протекает один и тот же ток. Точки соединения ветвей образуют узлы. Ветви вместе с узлами образуют контуры – замкнутые пути, по которым течёт ток.

Формулировка правил

Каждое правило Кирхгофа обладает универсальными свойствами. Как первое, так и второе, хоть и не относятся к фундаментальным законам, но твёрдо обоснованы.

Определения

Прежде, чем рассматривать простые принципы и смысл решения СУ (систем уравнений), нужно определиться с применяемыми формулировками. В типологии цепей пользуются следующими понятиями:

• ветвь;
• узел;
• контур.

Всё это – элементы электрической цепи (ЭЦ).

Элементы ЭЦ

Часть электроцепи, через которую проходит электричество одной и той же величины, называется ветвью. Место, в котором соединяются три и более ветви, именуют узлом. Обычно на схемах узлы обозначаются крупными точками. Контуром называется путь, по которому протекает электрический ток, проходя через несколько участков ЭЦ, включающих в себя узлы и ветви.

Важно! Ток (I), выходя из одной точки контура и единожды проходя по разветвлениям и узлам, должен обязательно вернуться в начало. Контур – это замкнутая цепь

Узлы и ветви, подлежащие изучаемому в определённый момент контуру, могут входить в состав других контуров: являться общими для нескольких замкнутых ЭЦ одновременно.

Первое правило

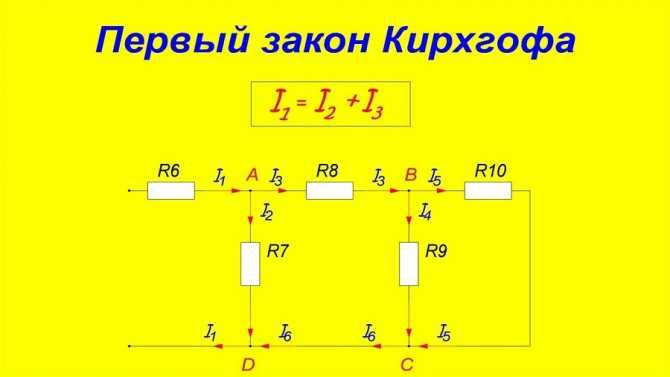
Первая закономерность Кирхгофа звучит так: «Сумма всех токов в узлах ЭЦ равна нулю». Если придать направление токам, текущим сквозь пересечения проводников, имеющих общий контакт (узел), то можно промаркировать стрелками, указывающими на узел, втекающие токи. Стрелками, имеющими направленность от узла, удобно отмечать вытекающие токи:

I1 + I2 – I3 – I4 – I5 = 0

Изображение направления движения электричества

Условно считая, что входящие I имеют плюсовой знак, а выходящие – минусовой, можно перефразировать утверждение. Согласно закону сохранения заряда, алгебраические суммы входящих в узел и выходящих из него I по значению равны.

Первый закон

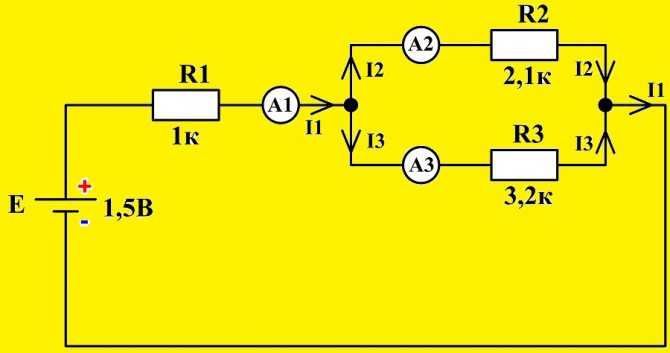
Убедиться в истинности первого правила можно, собрав смешанную схему включения резисторов, в качестве нагрузки, для источника питания U = 3 В.

Включенные в ветви амперметры позволяют визуально зафиксировать значения токов, входящих и выходящих из первого узла. Их алгебраическая сумма (учитывая знаки) будет равна нулю.

Схема цепи с установкой амперметров

Второе правило

Его называют правилом напряжений, оно утверждает, что сумма всех E (ЭДС), входящих в контур, равняется сумме падений напряжений на резистивных элементах, при условии, что контур замкнутый:

ΣE = ΣI*R.

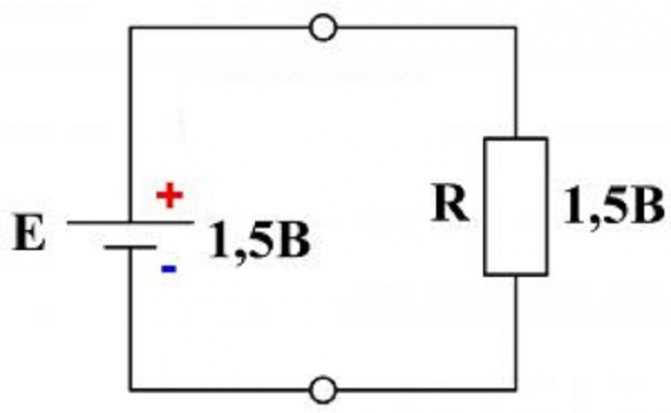
Например, для цепи с элементом питания и резистором напряжение на резисторе U = I*R будет равно ЭДС батарейки. По второму определению Кирхгофа выражение будет иметь вид:

E = I*R.

Схема с одной ЭДС и одним резистором

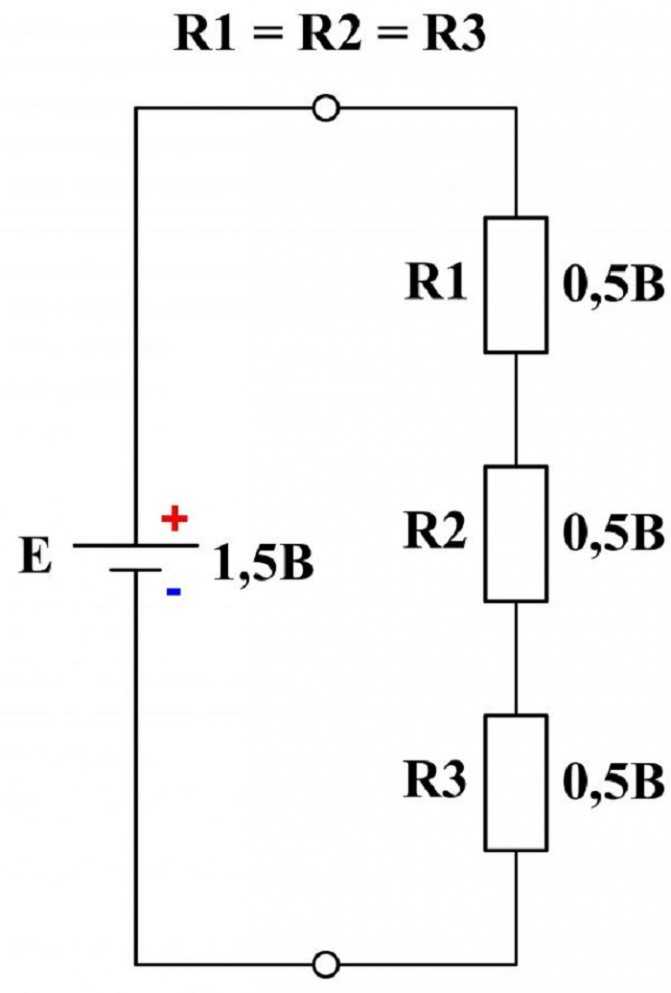
По аналогии, если количество резисторов увеличить, то падение напряжения на них распределится так, что в сумме они сравняются со значением ЭДС источника питания:

E = I*R1 + I*R2 + I*R.

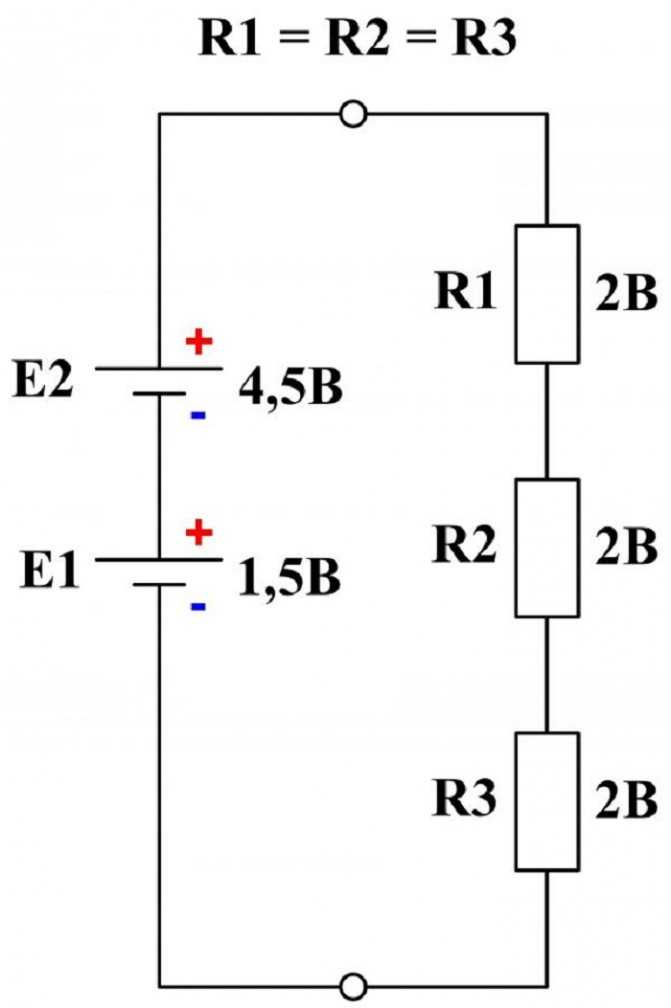
Включение одной ЭДС и трёх резисторов одного номинала

Объяснение было бы не полным, если не рассмотреть схему с несколькими ЭДС, входящими в контур. В этом случае выражать равенство следует следующим образом:

E1 + E2 = I*R1 + I*R2 + I*R3.

К сведению. При подключении нескольких источников в один контур необходимо соблюдать полярность, выполняя последовательное соединение плюса одного источника с минусом другого, таким образом, значения ЭДС будут суммироваться.

Включение двух источников в контур