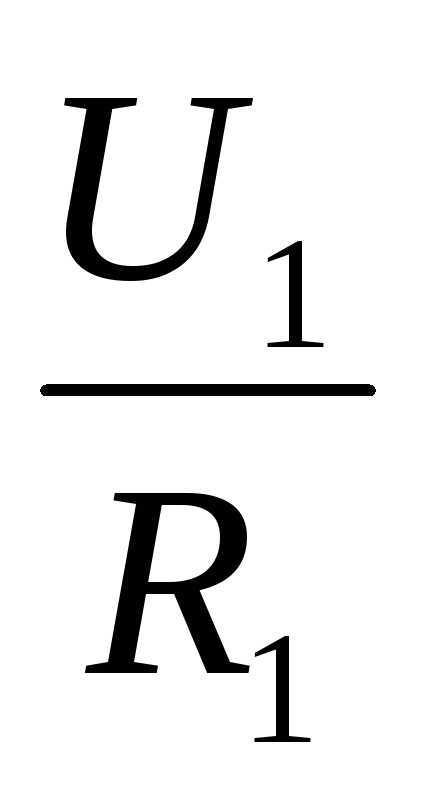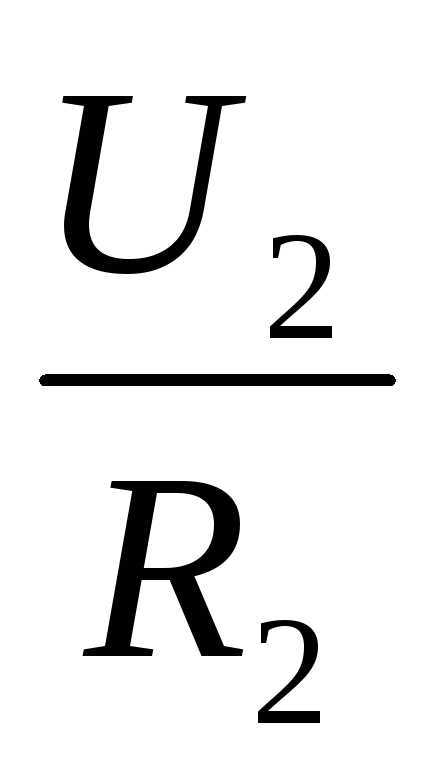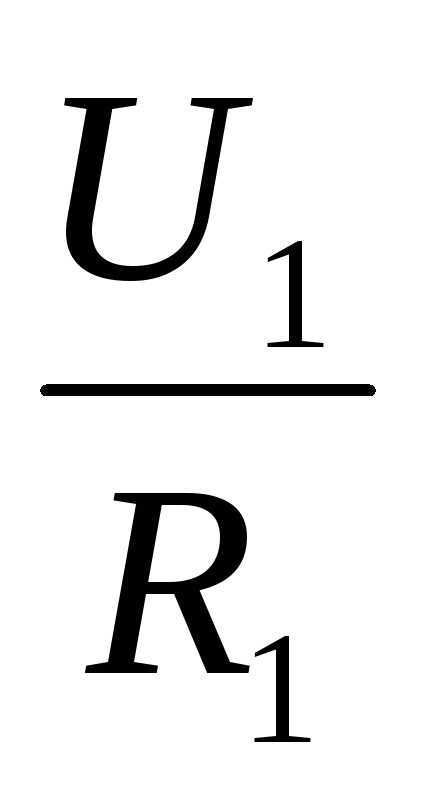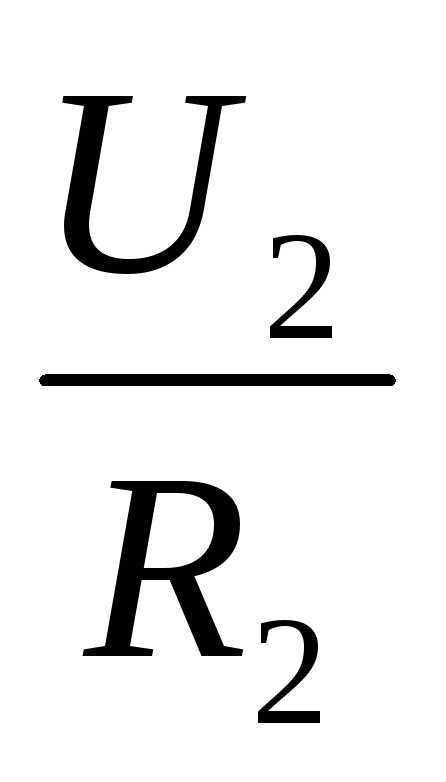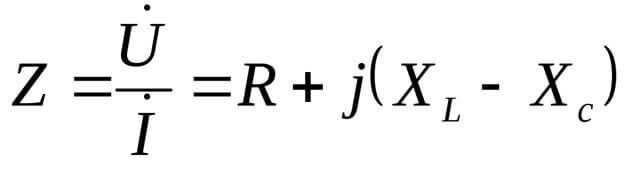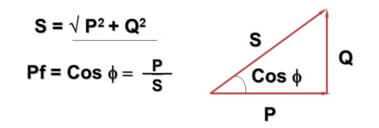Последовательное и параллельное включение элементов
Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение.
Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.
Цепь последовательно включенных резистивных элементов
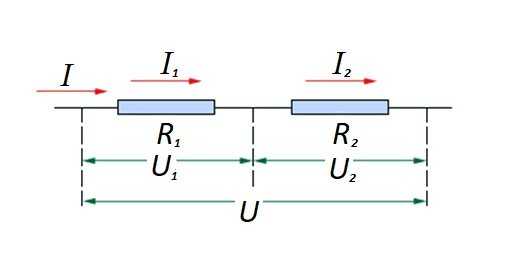
Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:
- I = I1 = I2 ;
- U = U1 + U2 ;
- R = R1 + R2
Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения.
Соединение резистивных элементов на участке схемы последовательно один с другим. Для этого варианта действует свой закон расчета. На схеме: I, I1, I2 – прохождение тока; R1, R2 – резистивные элементы; U, U1, U2 – приложенное напряжение
Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.
При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx.
Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.
Цепь параллельно включенных резистивных элементов
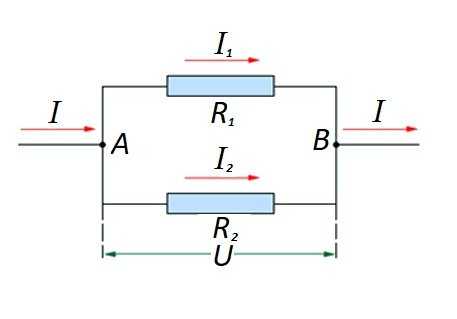
На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:
- I = I1 + I2 … ;
- U = U1 = U2 … ;
- 1 / R = 1 / R1 + 1 / R2 + …
Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение.
Соединение резистивных элементов на участке цепи параллельно один с другим. Для этого варианта применяется свой закон расчета. На схеме: I, I1, I2 – прохождение тока; R1, R2 – резистивные элементы; U – подведённое напряжение; А, В – точки входа/выхода
Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.
Интегральная и дифференциальная формы закона
Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры.
Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.
Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.
Под дифференциальный расчет берется формула: J = ό * E
Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ
Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.
Кельнский период
В этом городе ученый проведет 9 лет. На новом месте его переполняли позитивные эмоции – удобное расписание занятий, отличное оборудование, добрые отношения с коллегами создавали отличный жизненный фон. Из-за появившегося свободного времени параллельно с преподаванием Ом всерьез занялся наукой. В сфере его интересов – процессы, происходящие в электрических цепях.
Но сперва Георг занялся своими приборами, многие из которых нуждались в ремонте. С характерной для него въедливостью он стал готовить аппаратуру для запланированных экспериментов. Ома все больше интересовала физика с ее многочисленными загадками, да и конкуренция в этой области была не столь сильна. Направление движения к намеченной цели ученый определял порой интуитивно, но очень точно. Он понял, что сначала необходимо овладеть способами количественного исследования явлений.
Признание в мире ученых
Слава пришла к нему в 1841 году, когда научное сообщество в Лондоне, удостоило его медали за неординарные усилия. Ом заслуживает членство в Королевском научном обществе в 1842 году. Ома признают полноправным членом Баварской академии наук в 1845 году. Ома избирают членом-корреспондентом в Берлинском институте и Туринской академии. Фактически именно в Британии единица сопротивления впервые присвоена по фамилии Ома. Эта единица одобрена в международным соглашением во Франции, и имя Ома становится бессмертным в мире.
Это интересно: 157,Герои Отечественной войны 1812 года: излагаем детально
Закон Ома для переменного тока
Вышеприведённые соображения о свойствах электрической цепи при использовании источника (генератора) с переменной во времени ЭДС остаются справедливыми. Специальному рассмотрению подлежит лишь учёт специфических свойств потребителя, приводящих к разновремённости достижения напряжением и током своих максимальных значений, то есть учёта фазового сдвига .
Если ток является синусоидальным с циклической частотой
ω
{\displaystyle \omega }
, а цепь содержит не только активные, но и реактивные компоненты (ёмкости , индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными:
U
=
I
⋅
Z
{\displaystyle \mathbb {U} =\mathbb {I} \cdot Z}
-
U = U
0 e
i
ωt
— напряжение или разность потенциалов, -
I
— сила тока, -
Z = Re
−i
δ
— комплексное сопротивление (электрический импеданс), -
R
= √ R a
2 + R r
2— полное сопротивление,
-
R r
= ωL
− 1/(ωC
)
— реактивное сопротивление (разность индуктивного и емкостного), -
R а
— активное (омическое) сопротивление, не зависящее от частоты, -
δ = − arctg (R r
/R a
)
— сдвиг фаз между напряжением и силой тока.
При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведён взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру,
U
=
U
0
sin
(ω
t
+
φ)
{\displaystyle U=U_{0}\sin(\omega t+\varphi)}
подбором такой
U
=
U
0
e
i
(ω
t
+
φ)
,
{\displaystyle \mathbb {U} =U_{0}e^{i(\omega t+\varphi)},}
что
Im
U
=
U
.
{\displaystyle \operatorname {Im} \mathbb {U} =U.}
Тогда все значения токов и напряжений в схеме надо считать как
F
=
Im
F
{\displaystyle F=\operatorname {Im} \mathbb {F} }
Говорят: «не знаешь закон Ома – сиди дома». Так давайте же узнаем (вспомним), что это за закон, и смело пойдем гулять.
Сочинения
(1787-1854) немецкий физик
Гёорг Симон Ом родился в Эрлангене в семье слесаря-ремесленника. Его отец с детства внушил своим сыновьям любовь к математике и физике. Окончив гимназию, Георг в 1805 году поступил в Эрлангенский университет, но проучился там всего лишь год, а затем с 1806 по 1809 год работал учителем в швейцарском городе Готштадте. В 1811 году он защитил докторскую диссертацию, подготовленную самостоятельно. Георг Симон Ом преподавал математику, затем физику в различных гимназиях: с 1813 по 1817 год — в Вам-берге, с 1817 по 1828 год — в Кельне. В промежутках между уроками он занимался гальваническими опытами, пытаясь выяснить, как зависит действие гальванической батареи от качества и от рода металла, из которого сделана замыкающая ее полюсы проволока.
В 1826 году Ом экспериментально открыл основной закон электрической цепи, связывающий между собой силу тока, электродвижущую силу и сопротивление. Этот закон — закон Ома — был сформулирован им в работе «Определение закона, по которому металлы проводят электричество». В 1827 году ученый обосновал его теоретически для участка и для полной цепи. В своей маленькой лаборатории в Кельне он соорудил конструкцию, состоявшую из висмутного стержня, впаянного между двумя медными проволоками. Опустив один из спаев в кипящую воду, а другой — в мелко наколотый лед, Георг Ом скоро пришел к выводу, что между движением электрического тока и водного потока в наклонном русле существует аналогия. Чем больше перепад уровней в русле и свободнее путь, тем поток воды сильнее. Так же происходит и с электрическим током: сила тока будет тем больше, чем большей электродвижущей силой обладает батарея и чем меньше сопротивление току на его пути. В этом же году Ом ввел понятия «электродвижущей силы», «падения напряжения» и «проводимости».
Закон Ома долгое время не находил себе применения, хотя установленные в нем количественные соотношения между параметрами электрической цепи открыли широкие возможности в изучении электричества. К результатам работ немецкого ученого относились благосклонно местные физики, но ни в одной другой стране они не были известны. В октябре 1831 года профессор прикладной физики Парижской школы искусств и ремесел Клод Серве Пулье сообщил Французской академии, что нашел количественное соотношение между током, электродвижущей силой и сопротивлением, не упоминая имени Ома. Но затем он был вынужден признать, что читал сочинение немецкого физика о гальванической цепи и согласен с тем, что этот закон первым сформулировал Георг Симон Ом. Эта скандальная история способствовала тому, что о работах Ома узнали и другие французские, а затем английские физики. Значение закона Ома стало несомненным только после того, как выдающиеся русские ученые Эмилий Христиано-вич Ленц и Борис Семенович Якоби, немецкие ученые Карл Фридрих Гаусс, Густав Роберт Кирхгоф и некоторые другие положили этот закон в основу своих исследований.
Несмотря на открытие количественного закона, Георг Ом продолжал оставаться скромным учителем. В возрасте 44 лет (в 1833 году) он получает место профессора физики Нюрнбергской высшей политехнической школы, а в 1839 году становится ее ректором. Лондонское королевское общество в 1841 году наградило его медалью Копли. В 1849 году ученого пригласили в Мюнхенский университет на должность экстраординарного профессора, а в 1852 году, когда Ому было 63 года, он стал профессором. Всю жизнь Георг Симон Ом был великим тружеником, но его преследовали неудачи.
Научные интересы Ома распространялись также и на акустику, оптику, кристаллооптику. Ему принадлежит мысль о сложном составе звуков. В частности, в 1843 году Ом установил, что простейшие слуховые ощущения вызываются лишь гармоническими колебаниями. Ухо способно разлагать сложные звуки на синусоидальные составляющие, и они воспринимаются как основной тон, и добавочные — обертоны. В этом состоит акустический закон Ома. Однако эти труды ученого признания не получили, и только через восемь лет после его смерти его соотечественник Герман Людвиг Фердинанд Гельмгольц смог доказать справедливость выводов Ома. Позже, основываясь на акустическом законе Ома, Гельмгольц разработал резонансную теорию слуха. В 1842 году Ом был избран членом Лондонского королевского общества.
В конце 40-х годов он задумал создать стройную теорию молекулярной физики. К сожалению, ученый успел написать и издать всего один том своего труда. 7 июля 1854 года он скоропостижно скончался.
Спустя двадцать семь лет после смерти Ома, когда его именем назвали общепринятую единицу сопротивления, «дорогому соотечественнику» в Мюнхене воздвигли памятник.
Открытия
Наиболее известные работы Ома касались вопросов о прохождении электрического тока и привели к знаменитому «закону Ома », связывающему сопротивление цепи электрического тока, напряжение и силу тока . В первой его учёной работе («Vorläufige Anzeige des Gesetzes, nach welchem Metalle die Contactelectricitätleiten», 1825) Ом опытно исследует эти явления, но, по несовершенству приборов, приходит к ошибочному результату. В последующей работе («Bestimmung des Gesetzes, nach welchem Metalle die Contactelektricitätleiten», 1826) Ом формулирует свой знаменитый закон и затем все свои работы по этому вопросу объединяет в книге: «Die galvanische Kette, mathematisch bearbeitet» (Б., 1827; переиздано Мозером в Лейпциге, 1887; переведено на языки английский в 1841 г., итальянский в 1847 г. и французский в 1860 г.), в которой даёт и теоретический вывод своего закона, исходя из теории, аналогичной теории теплопроводности Фурье
Несмотря на важность этих работ они прошли незамеченными и были встречены даже враждебно, и лишь когда Пулье во Франции снова пришёл (1831-37), опытным путём, к тем же результатам, закон Ома был принят учёным миром, и Лондонское королевское общество на заседании 30 ноября 1841 г. наградило Ома медалью Копли
Открытие Ома, давшее впервые возможность количественно рассмотреть явления электрического тока, имело и имеет огромное значение для науки; все теоретические (Гельмгольц) и опытные (Бетц, Кольрауш, комиссия британской ассоциации) проверки показали полную его точность; закон Ома есть истинный закон природы.
Дальнейшие работы Ома по электричеству касались вопросов униполярной проводимости (1830) и нагревания проводов током (1829). В 1839 г
последовал ряд работ по акустике, приведших к результатам большой важности. В статье «Ueber die Definition des Tones nebst daran geknüpfter Theorie der Sirene und ähnlicher tonbildender Vorrichtungen» (1843) высказан закон (тоже называемый «законом Ома»), что человеческое ухо познаёт лишь простые гармонические колебания, и что всякий сложный тон разлагается ухом на составные (по закону Фурье) и познается лишь как сумма их
И этот закон не был принят современниками Ома, и лишь Гельмгольц, через восемь лет после смерти Ома, доказал его полную справедливость.
Закон Кирхгофа
Пусть имеется произвольная разветвленная сеть проводников. В отдельных участках включены разнообразные источники тока. ЭДС источников постоянны и будем считать известными. При этом токи во всех участках цепи и разности потенциалов на них можно вычислить при помощи закона Ома и закона сохранения заряда.
Для упрощения решения задач по расчетам разветвлённых электрических цепей, имеющих несколько замкнутых контуров, несколько источников ЭДС, используют законы (или правила) Кирхгофа. Правила Кирхгофа служат для того, чтобы составить систему уравнений, из которой находят силы тока в элементах сложной разветвленной цепи.
Первый закон Кирхгофа
Сумма токов в узле цепи с учетом их знаков равна нулю:
Первое правило Кирхгофа является следствием закона сохранения электрического заряда. Алгебраическая сумма токов, сходящихся в любом узле цепи — это заряд, который приходит в узел за единицу времени.
При составлении уравнение используя законы Кирхгофа важно учитывать знаки с которыми силы токов входят в эти уравнения. Следует считать, что токи, идущие к точке разветвления, и исходящие от разветвления имеют противоположные знаки
При этом нужно для себя определить какое направление (к узлу или от узла) считать положительным.
Второй закон Кирхгофа
Произведение алгебраической величины силы тока (I) на сумму вешних и внутренних сопротивлений всех участков замкнутого контура равно сумме алгебраических значений сторонних ЭДС () рассматриваемого контура:
Каждое произведение определяет разность потенциалов, которая существовала бы между концами соответствующего участка, если бы ЭДС в нем была равно нулю. Величину называют падением напряжения, которое вызывается током.
Второй закон Кирхгофа иногда формулируют следующим образом:
Для замкнутого контура сумма падений напряжения есть сума ЭДС в рассматриваемом контуре.
Второе правило (закон) Кирхгофа является следствием обобщенного закона Ома. Так, если в изолированной замкнутой цепи есть один источник ЭДС, то сила тока в цепи будет такой, что сумма падения напряжения на внешнем сопротивлении и внутреннем сопротивлении источника будет равна сторонней ЭДС источника. Если источников ЭДС несколько, то берут их алгебраическую сумму. Знак ЭДС выбирается положительным, если при движении по контуру в положительном направлении первым встречается отрицательный полюс источника. (За положительное направление обхода контура принимают направление обхода цепи либо по часовой стрелке, либо против нее).
Закон Ома в дифференциальной форме
Параллельное соединение резисторов
Представленные выше объяснения справедливы для случаев, когда замыкать будут цепь из однородного материала с неизменным поперечным сечением по всей длине. Такими характеристиками обладает обычный провод, сделанный из металла с минимальным количеством посторонних примесей. Качественный резистор обладает аналогичными параметрами. Производители обеспечивают не только равномерное распределение сопротивления в объеме элемента. Дополнительными особенностями конструкции минимизируют реактивные составляющие, чтобы исключить искажения при подключении источника переменного сигнала. Однако даже использование постоянного тока в отдельных ситуациях не позволяет применять для расчетов рассмотренные методики.
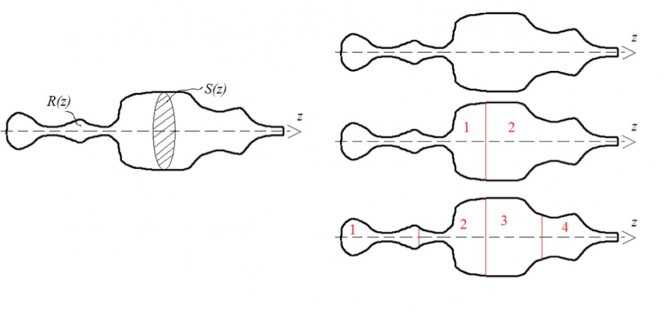
Проводник с различным сопротивлением вдоль продольной оси
Для удобства можно рассмотреть представленный на картинке образец. В действительности необязательно изменение геометрии проводника по пути прохождения тока. На электрическое сопротивление оказывают влияние различные примеси, существенно различающиеся температурные режимы на протяжении линии определенной цепи.
Для определения электрических параметров классическая формула Ома преобразуется в дифференциальную форму. В данном примере рассматривается изменение площади поперечного сечения S и сопротивления R при перемещении зоны наблюдения вдоль продольной оси. Чтобы упростить расчет, принимают равномерное распределение материала и незначительное содержание посторонних примесей.
Дифференциальный способ, как показано на картинке, заключается в последовательном делении области эксперимента на мелкие участки. Продолжив процесс, на определенном уровне можно получить цилиндр с бесконечно малой толщиной. В таком образце площадь поперечного сечения будет неизменной. Для расчета используют выражение зависимостей:
J = p*E, где:
- J (E) – векторные выражения плотности тока (напряженности);
- p (табличное значение из справочника) – удельная проводимость материала.
Формулировка закона Ома для полной цепи
Закон Ома для полной цепи выражается поведением основных величин, был выведен опытным экспериментальным путем. Результатом стало выявление связей, объединяющих силу тока (I), электродвижущую силу – ЭДС (Е), внешнее (R) и внутреннее (r) сопротивления в цепи.
В теоретических расчетах с точки зрения чистой физики, в цепях предполагался так называемый идеальный источник постоянного тока. После того, как были проведены реальные исследования, выяснилось, что источник тока обладает собственным сопротивлением.
Следует сразу же выяснить, что такое электродвижущая сила. По сути, она является физической величиной, характеризующей действие внешних сил источника ЭДС. Например, в простой батарейке перемещение зарядов происходит в результате химической реакции. То есть, данная сила двигает заряд, обеспечивая общее течение электрического тока.
Исследования и публикации
Его сочинения были многочисленны. В своей первой статье 1825 года Ом рассматривает уменьшение электромагнитной силы, создаваемой проводом, по мере увеличения длины провода. В 1826 году он дал описание проводимости в схемах, смоделированных на основе исследования теплопроводности Фурье. Эта статья продолжает вывод Ома результатов из экспериментальных данных, и, особенно во втором случае, он смог предложить законы, которые во многом помогли объяснить результаты других, работающих над гальваническим электричеством
Самой важной была его брошюра, опубликованная в Берлине в 1827 году, под названием Die galvanische Kette Mathematisch Bearbeitet.. Эта работа, зародыши которой появились в течение двух предшествующих лет в журналах Швайггера и Поггендорфа, оказала важное влияние на развитие теории и приложений электрического тока
Имя Ома было включено в терминологию электротехники в Законе Ома (который он впервые опубликовал в Die galvanische Kette …) о пропорциональности тока и напряжения в резисторе , и принят как единица измерения сопротивления в системе СИ , Ом (символ Ω).
Хотя работа Ома сильно повлияла на теорию, поначалу она была воспринята без особого энтузиазма. Тем не менее, его работа была в конечном итоге признана Королевским обществом, награжденным медалью Копли в 1841 году. Он стал иностранным членом Королевского общества в 1842 году, а в 1845 году он стал действительным членом Баварской академии наук. и гуманитарные науки
В какой-то степени Чарльз Уитстон обратил внимание на определения, которые Ом ввел в области физики
Работает
Grundlinien zu einer zweckmäßigen Behandlung der Geometrie als höheren Bildungsmittels an vorbereitenden Lehranstalten / entworfen ( Рекомендации по правильному обращению с геометрией в высших учебных заведениях в подготовительных институтах / примечания )
Die galvanische Kette: Mathematisch Bearbeitet ( Гальваническая цепь, исследованная математически )
Elemente der analytischen Geometrie im Raume am schiefwinkligen Coordinatensysteme ( Элементы аналитической геометрии, касающиеся косой системы координат )
Grundzüge der Physik als Compendium zu seinen Vorlesungen ( Основы физики: Сборник лекций )
Библиография и PDF-файлы всех статей и книг Георга Симона Ома
Поздние годы
В 1826 г. Кёльнская иезуитская гимназия предоставляет Ому отпуск с сохранением половины оклада для продолжения его научных исследований, но, в сентябре 1827 г., учёный вынужден вновь приступить к своим учительским обязанностям. Весь год, проведённый в Берлине, он искренне верил в то, что его научная публикация поможет получить достойное место в каком-нибудь известном университете. Однако когда этого не произошло, он неохотно возвращается на прежнее место работы
Но самым худшим во всей истории было то, что, несмотря на всю важность его работы, научный мир принял её более чем прохладно. Оскорблённый, Ом решает переехать в Берлин
И в марте 1828 г. он официально оставляет свой пост в Кёльнской иезуитской гимназии и устраивается на временную работу учителем математики в разные школы Берлина. В 1833 г. учёный принимает предложение занять пост профессора в Нюрнберге. Но, даже получив заветную должность, Ом остаётся недоволен. Упорные и тяжёлые труды учёного были, наконец, вознаграждены в 1842 г., когда он получает медаль Копли Британского королевского общества. Уже в следующеем году его избирают иностранным членом общества. В 1845 г. Ом становится полноправным членом Баварской академии. Еще четыре года спустя, он занимает должность куратора музея физики при Баварской академии в Мюнхене и читает лекции в Мюнхенском университете. Лишь в 1852 г. Ом получит должность, к которой стремился всю свою жизнь: его назначают главой кафедры физики Мюнхенского университета.
Семья и последние годы
Георг Ом из-за своей занятости не имел семью и детей. Он умер 6 июля 1854 года в своей квартире, во время работы над учебником по оптике. Его похоронили на кладбище в Мюнхене, в Судлихе Фридхоф. На его могиле изображен символ единицы сопротивления, так же указана ошибочная дата его рождения, он родился не в 1787 году, а в 1789 году.
Закон ома определение
Закон Ома для полной цепи: история и формулы.
Что же собой представляет закон Ома для полной цепи? Итак, это формула, в которой наглядно видна связь основных параметров электрической цепи: тока, напряжения и сопротивления. Для того чтобы понять суть закона, давайте для начала разберемся с некоторыми понятиями.
Что называют электрической цепью?
Электроцепь – это путь в электрической схеме, которым протекают заряды (электрические элементы, провода и другие устройства). Конечно же, ее началом считается источник электропитания. Под воздействием электромагнитного поля, фотонных явлений или химических процессов электрические заряды стремятся перейти на противоположную клемму этого источника электропитания.
Что такое электрический ток?
Направленное движение заряженных частиц при воздействии на них электрического поля либо других сторонних сил и называется электрическим током. Его направление определяется направленностью протонов (положительных зарядов). Ток будет постоянным, если с течением времени не изменилась ни его сила, ни направление.
История закона Ома
При проведении экспериментов с проводником физику Георгу Ому удалось установить, что сила тока пропорциональна напряжению, которое приложено к его концам:
I / sim U или I = G / U,
где G – электропроводность, а величина R = 1 / G – электрическое сопротивление проводника. Это открытие было установлено знаменитым немецким физиком в 1827 году.
Законы Ома
Для полной цепи определение будет следующим: сила тока в электроцепи равна отношению электродвижущей силы (далее ЭДС) источника к сумме сопротивлений:
I = E / (R + r),
где R – сопротивление внешней цепи, а r – внутреннее сопротивление источника тока. Довольно часто формулировка закона вызывает затруднения, поскольку не всем знакомо понятие ЭДС, ее отличие от напряжения, далеко не все знают, что означает и откуда появляется внутреннее сопротивление. Для этого и нужны пояснения, ведь закон Ома для полной цепи имеет глубокий смысл.
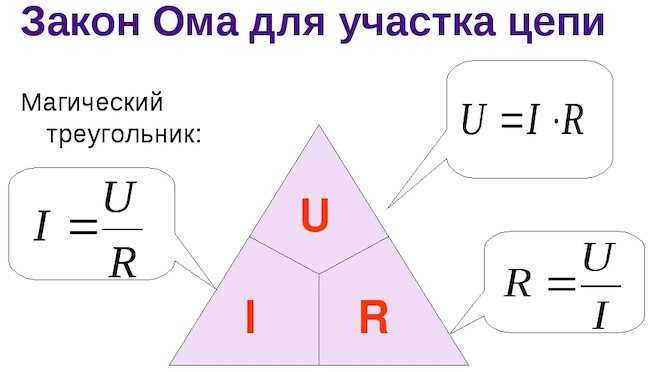
Формулировку закона для участка цепи можно назвать прозрачной. Речь идет о том, что для ее понимания не нужны дополнительные разъяснения: ток в цепи прямо пропорционален напряжению и обратно пропорционален сопротивлению:
I = U / R.
Смысл
Закон Ома для полной цепи прочно связан с законом сохранения энергии. Давайте предположим, что источник тока не имеет внутреннего сопротивления. Что же в таком случае должно происходить? Оказывается, если бы отсутствовало сопротивление, то во внешнюю цепь отдавался бы ток большей величины, соответственно и мощность была бы большей.
Теперь пришло время разобраться с понятием электродвижущей силы. Эта величина представляет собой разность между электрическими потенциалами на клеммах источника, но только без какой-либо нагрузки. В качестве примера давайте возьмем напор воды в приподнятом баке. Уровень воды будет находиться на месте, пока ее не начнут расходовать. При открытии крана уровень жидкости будет уменьшаться, поскольку нет подкачки. Попадая в трубу, вода испытывает сопротивление, то же самое происходит и с электрическими зарядами в проводе.
При отсутствии нагрузок, клеммы находятся в разомкнутом состоянии, получается, что ЭДС и напряжение совпадают по величине. Если же мы, к примеру, включим лампочку, цепь замкнется, а электродвижущая сила создаст напряжение в ней, выполняя полезную работу. Часть энергии из-за внутреннего сопротивления рассеется (это называют потерями).
В том случае, если сопротивление потребителя меньше внутреннего, то на источнике тока выделяется большая мощность. И тогда происходит падение ЭДС во внешней цепи, а на внутреннем сопротивлении теряется существенная часть энергии. Суть законов сохранения заключается в том, что природа не может взять больше, чем отдать.
Хорошо знакома сущность внутреннего сопротивления обитателям «хрущевок», у которых в квартирах имеются кондиционеры, а старая проводка так и не была заменена. Электрический счетчик вращается с бешеной скоростью, нагревается розетка и стена в тех местах, где проходят старые алюминиевые провода, в результате чего кондиционер еле-еле охлаждает воздух в помещении.
Природа r
«Полный Ом» (как привыкли закон называть электрики) плохо понимается, поскольку у внутреннего сопротивления источника, как правило, не электрическая природа. Давайте разберемся с этим на примере солевой батарейки. Известно, что электриче
Использование на практике
Закон Ома лежит в основе всех расчетов производимых в электронике и электротехнике. Будущих специалистов с первых дней учат, как использовать так называемый треугольник. Чтобы найти какую-то искомую величину, должны выполняться простые арифметические действия. Если два оставшихся параметра находятся в одной строке – они перемножаются. Если на разных уровнях, то верхний всегда делится на нижний.
Самые простые вычисления производятся на основе данных измерительных приборов. На участке цепи измерение тока выполняется амперметром, а напряжения – вольтметром. После этого найти сопротивление математическим путем не составит труда.
Для замеров сопротивления тоже есть прибор – омметр. Полученное выражение, подставляется в одну из формул, после чего находятся величины силы тока или напряжения. Точность омметра зависит от стабильности напряжения, подаваемого источником тока. Стабилизация проводится путем добавления резистора, выполняющего функцию регулятора.
Иногда требуется исключить из схемы какой-нибудь элемент без демонтажа. С этой целью проводится шунтирование, когда приходится устанавливать проводник на входных клеммах ненужного резистора. Ток начинает идти через шунт с меньшим сопротивлением, а напряжение на резисторе падает до нуля.
Закон Ома используется в защитных системах. Это делается с помощью уставок, обеспечивающих нормальную работу и отключающих питание лишь в аварийных ситуациях.
Закон Ома для переменного тока
При расчете цепей переменного тока вместо понятия сопротивления вводят понятие «импеданс». Импеданс обозначают буквой Z, в него входит активное сопротивление нагрузки R a и реактивное сопротивление X (или R r). Это связано с формой синусоидального тока (и токов любых других форм) и параметрами индуктивных элементов, а также законов коммутации:
- Ток в цепи с индуктивностью не может измениться мгновенно.
- Напряжение в цепи с ёмкостью не может измениться мгновенно.
Таким образом, ток начинает отставать или опережать напряжение, и полная мощность разделяется на активную и реактивную.
X L и X C – это реактивные составляющие нагрузки.
В связи с этим вводится величина cosФ:
Здесь – Q – реактивная мощность, обусловленная переменным током и индуктивно-емкостными составляющими, P – активная мощность (выделяется на активных составляющих), S – полная мощность, cosФ – коэффициент мощности.
Возможно, вы заметили, что формула и её представление пересекается с теоремой Пифагора. Это действительно так и угол Ф зависит от того, насколько велика реактивная составляющая нагрузки – чем её больше, тем он больше. На практике это приводит к тому, что реально протекающий в сети ток больше чем тот, что учитывается бытовым счетчиком, предприятия же платят за полную мощность.
При этом сопротивление представляют в комплексной форме:
Здесь j – это мнимая единица, что характерно для комплексного вида уравнений. Реже обозначается как i, но в электротехнике также обозначается и действующее значение переменного тока, поэтому, чтобы не путаться, лучше использовать j.
Мнимая единица равняется √-1. Логично, что нет такого числа при возведении в квадрат, которого может получиться отрицательный результат «-1».